1.贝努里队列概述

贝努里队列是一个森林，森林中每颗树（贝努里树）都有一定约束，但不是有顺序性的二叉树。

贝努里树是满足堆的有序性的树。

1.1.贝努里队列案例

贝努里树有高度，高度为0的贝努里树有1个结点，高度为n的贝努里树有2^n个结点。下图是简单的贝努里队列。

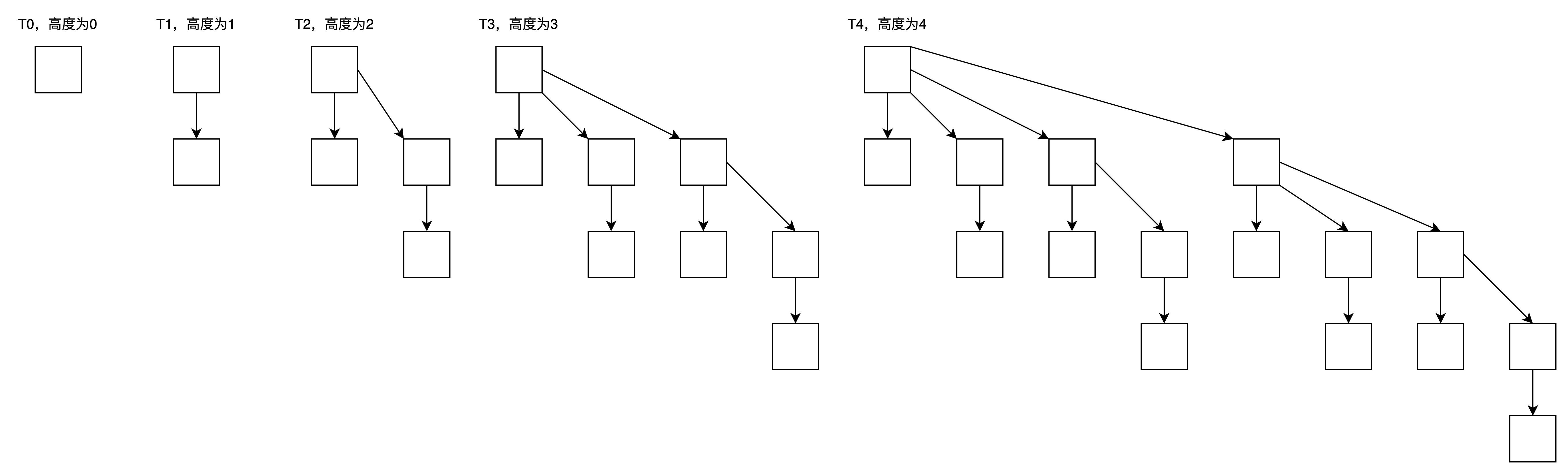
队列中有5颗贝努里树，高度分别为0、1、2、3、4。共容纳了2^0 + 2^1 + 2^2 + 2^3 + 2^4 = 31个结点。

1.2.贝努里树

贝努里树不是二叉树，是一颗普通的树，但每颗树的根结点都比树中其他结点要大或者小，满足最大堆或最小堆的有序性。

1.3.贝努里队列的存储

贝努里队列中每颗树可以采用儿子兄弟链的方式存储，每颗树都有一个根结点，贝努里队列用一个数组来存储所有树的根结点指针，数组0号元素指向T0的根结点，数组1号元素指向T1的根结点。

2.贝努里队列运算

贝努里队列最基本的操作是归并、入队和出队，其中归并是基础，入队和出队操作都可以看成是一种特殊的归并。

2.1.归并

因为贝努里队列的特性，高度为n的贝努里树有2^n个结点，所以归并操作看起来像是一个二进制的加法。

2.1.1.归并规则

根据贝努里树的高度，从低到高依次归并两个高度相同的树。

2.1.2.最小堆归并算法

在归并两颗高度相同的树时，只需要将根结点较大的树作为根结点较小的树的子树。

2.1.3最大堆归并算法

在归并两颗高度相同的树时，只需要将根结点较小的树作为根结点较大的树的子树。

2.2.入队

入队是归并的特例。入队的结点可以看成是一颗只有一个结点的贝努里树，然后进行归并。

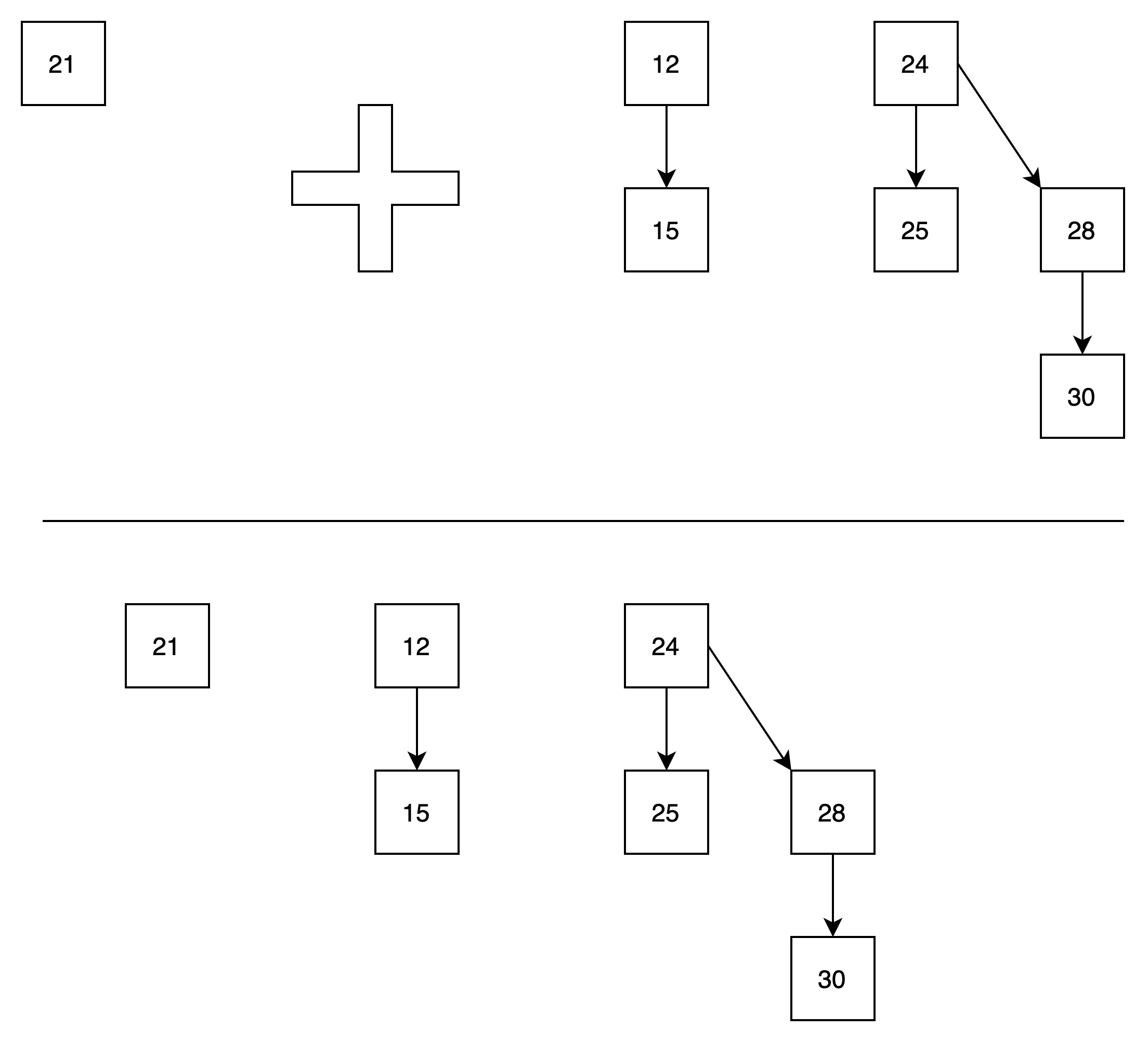
2.2.1.最好的情况入队

最好的情况下，贝努里队列中没有高度为0的树，则插入的结点就是组成高度为0的树。此场景下，操作时间复杂度为O(1)。如下图所示：

2.2.2.最坏情况入队

最坏的情况下，贝努里队列中有2^n - 1个结点，也就有n个高度（从0到n-1），则需要归并n-1次，最终形成一颗高度为n的贝努里树。此场景下，操作时间复杂度为O(logN)。

下面通过案例来说明最坏情况下的入队。

（1）将元素9入队，

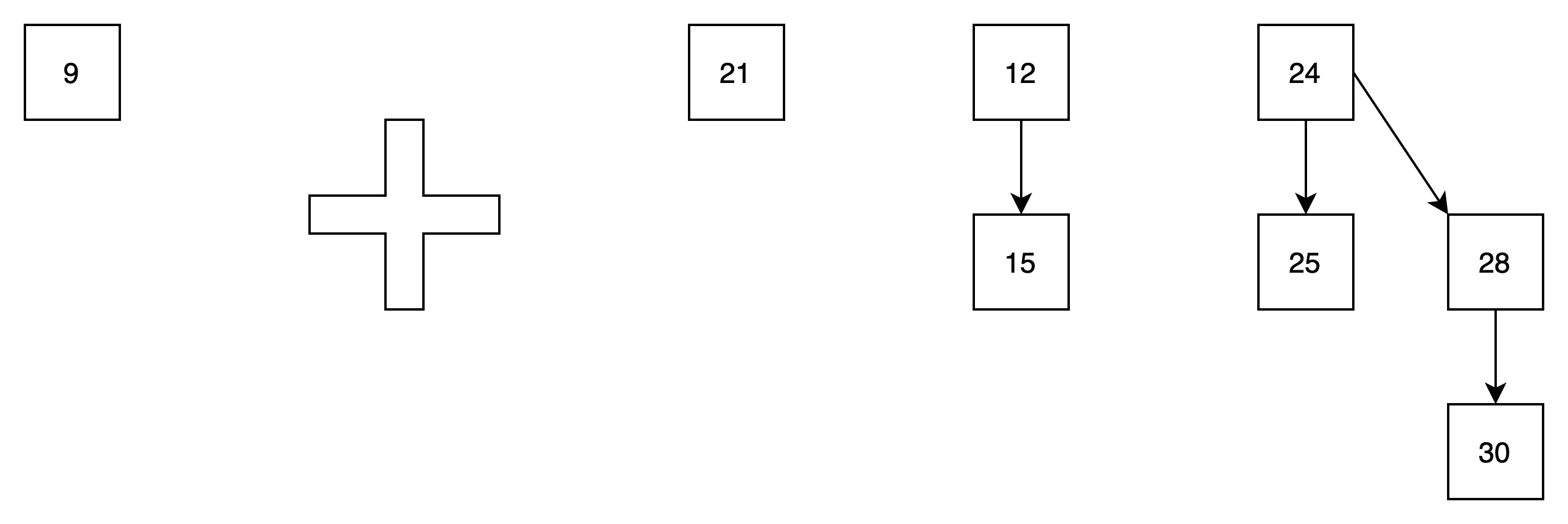
可以看成一颗高度为0的树与贝努里队列的归并

（2）将两个高度为0的贝努里树归并，得到以下结果

形成一个新的高度为1的贝努里树

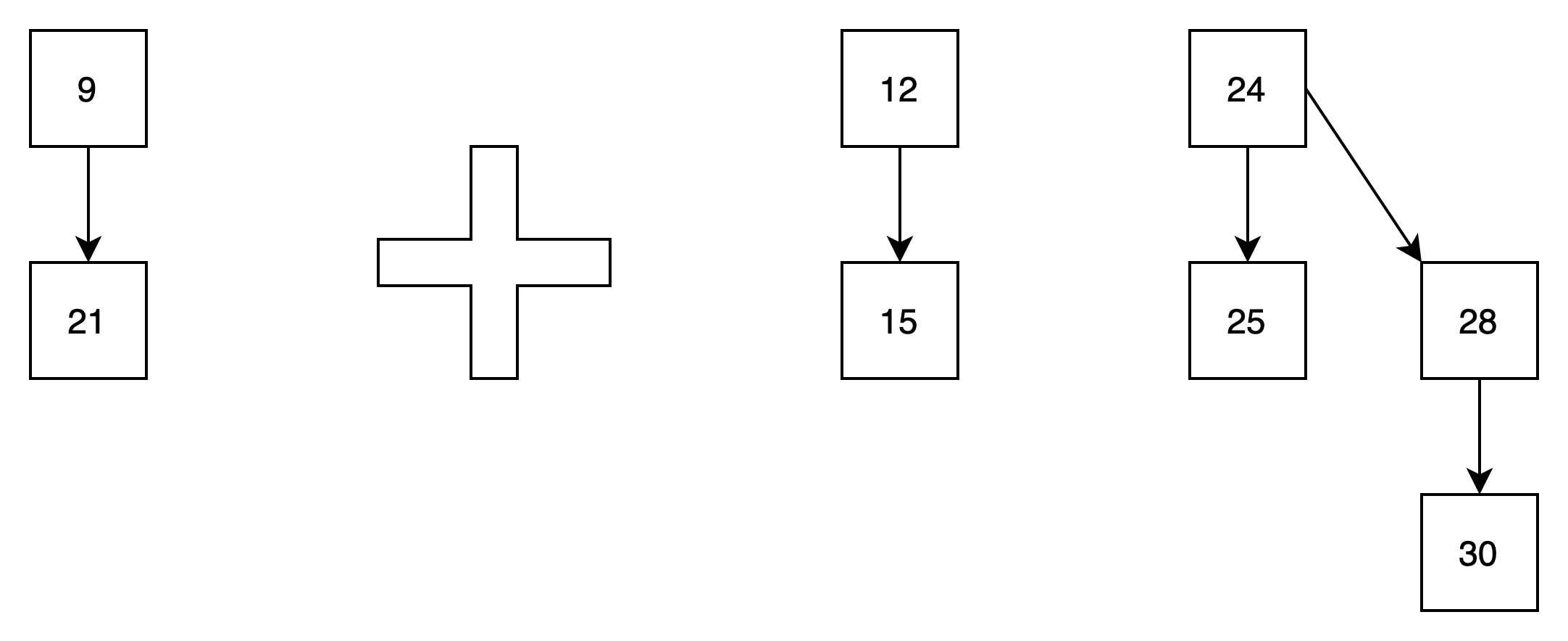
（3）将两个高度为1的贝努里树归并，得到以下结果

新成一个新的高度为2的贝努里树

（4）将两个高度为2的贝努里树归并，得到以下结果

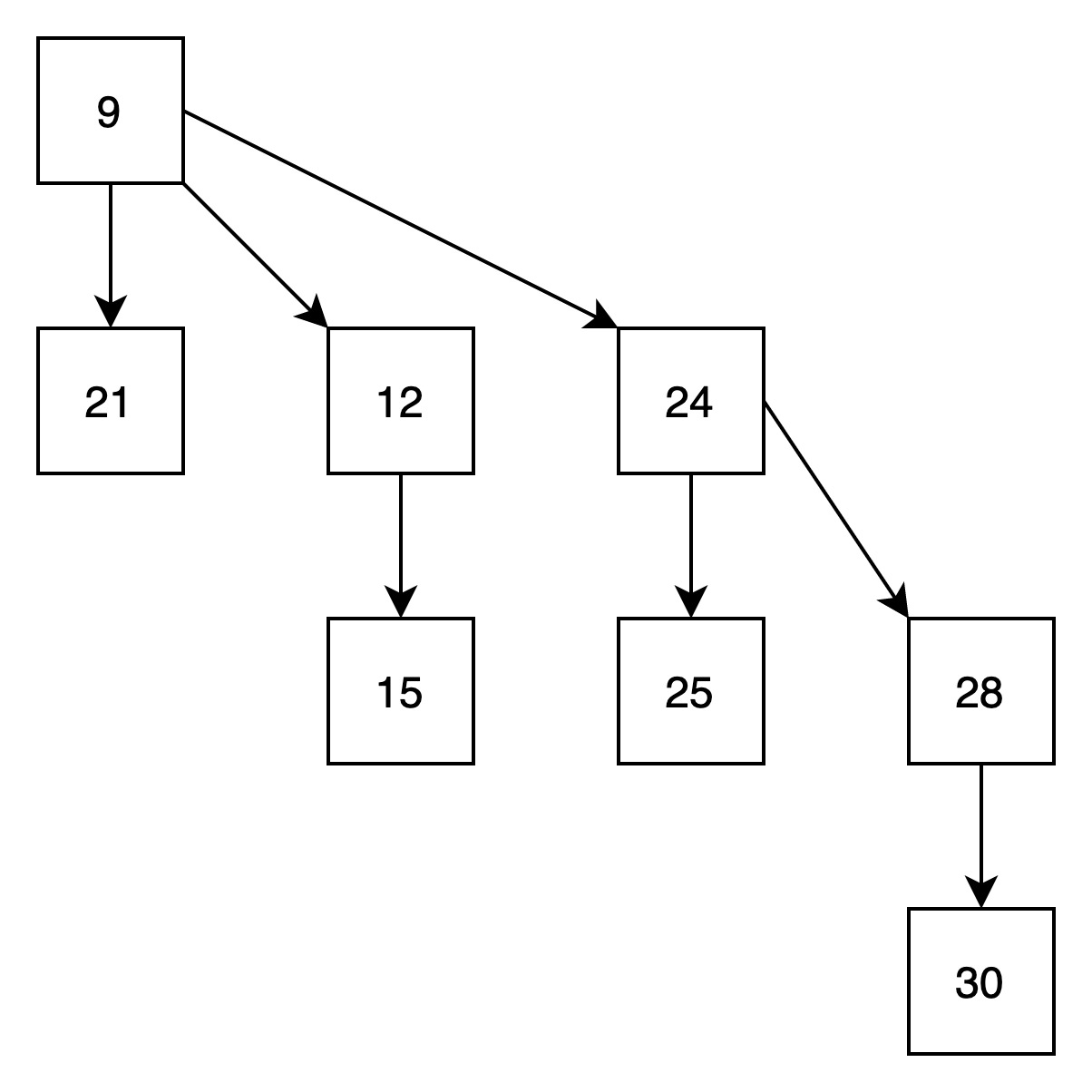
归并完成，最终得到一颗高度为3的树。最终进行了三次归并。

2.2.3.入队平均时间复杂度

并不是每次都是最坏的情况，如果把每颗树的出现看成是等概率的，即50%，那么平均归并两次就能结束。所以归并操作的平均时间复杂度是O(1)。

2.3.出队

出队也可以看成是一种特殊的归并。

2.3.1.出队算法

算法过程如下：

（1）在贝努里队列中找到根结点最小（大）的树T

（2）将T从原森林中删除

（3）在T中删除根结点，就形成了一片由贝努里树组成的森林F

（4）将森林F中的每一棵树与原森林进行归并

在第（1）步中考虑最大堆和最小堆。

2.3.2.出队时间复杂度

在出队过程中，首先在队列中找到根结点找到最小的树，需要花费O(logN)的时间。然后又要归并两个优先级队列，也需要花费O(logN)的时间。

所以，出队的时间复杂度为O(logN)。

2.3.3.出队案例

下面通过案例来说明出队过程，以最小堆为例。

（1）准备一个贝努里队列

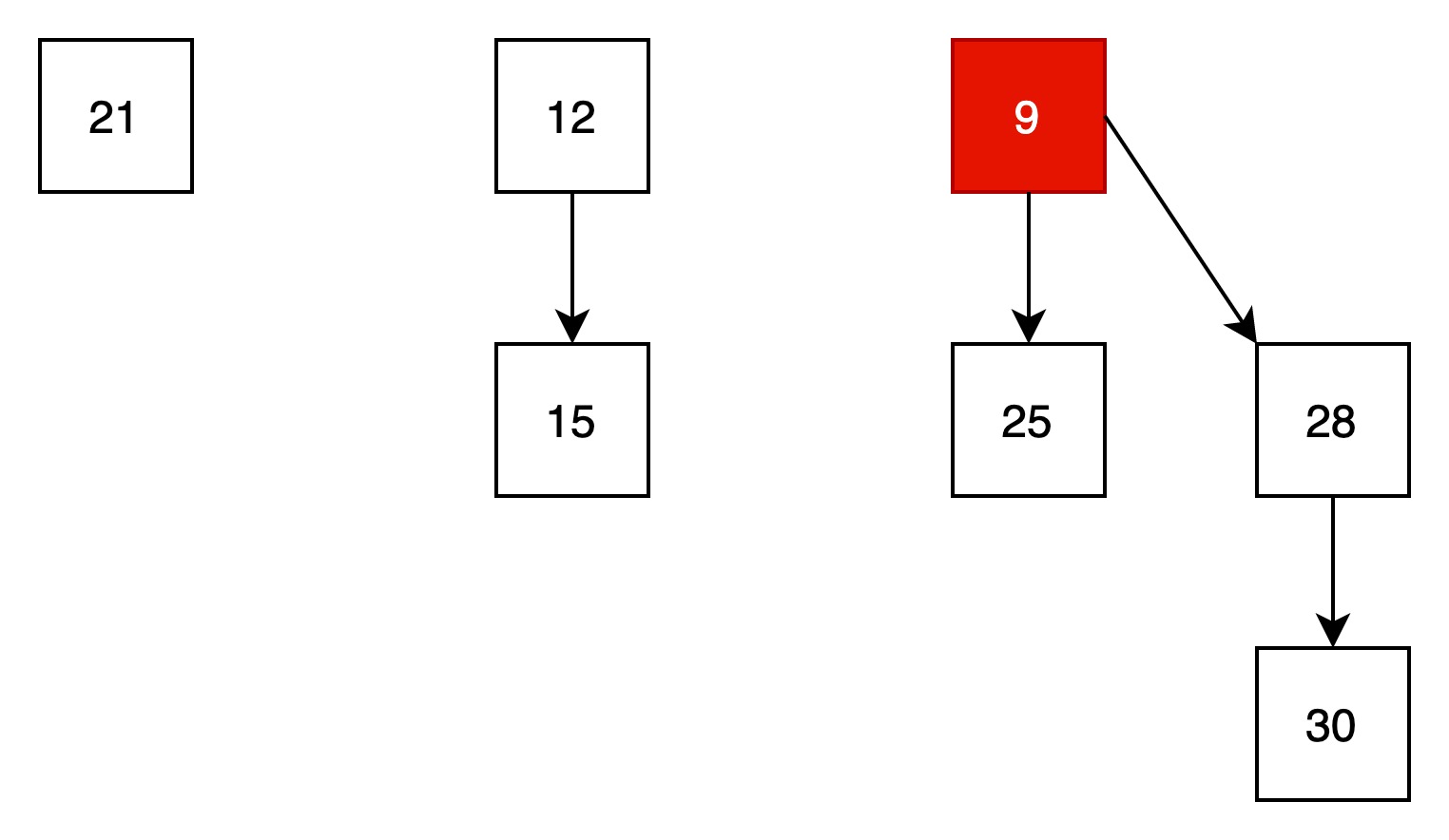
（2）找到最小值，并将最小值从贝努里队列中删除

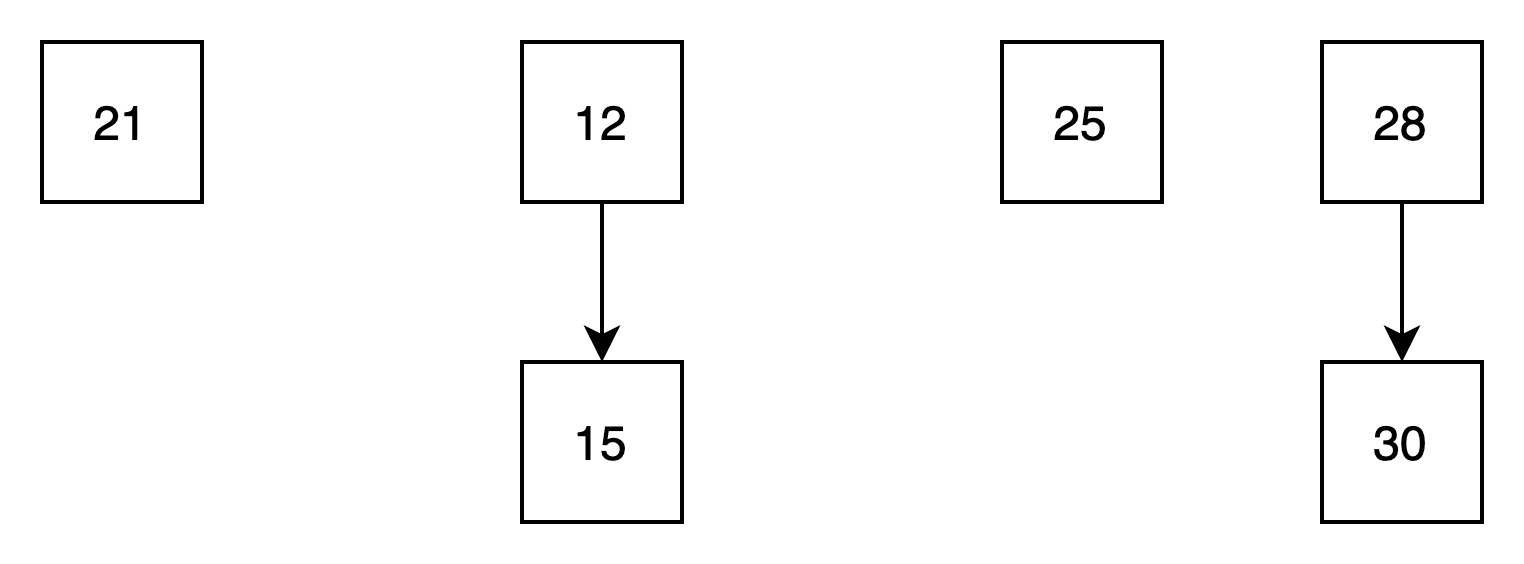
得到两颗高度为0的树，以及两颗高度为1的树。

（3）将森林中的树进行归并

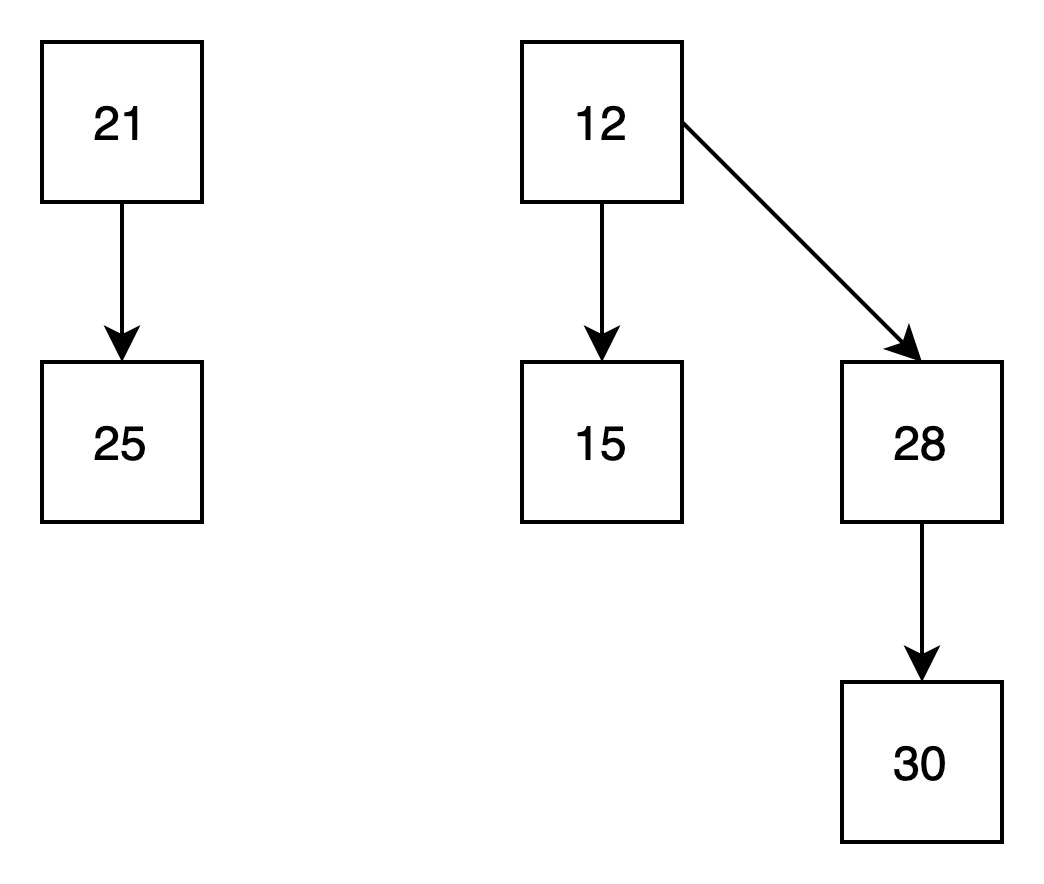
对两颗高度为0的树和两颗高度为1的树进行归并。最终得到一颗高度为1的树，和一颗高度为2的树。