1.斜堆的定义

斜堆是满足堆的有序性，但是没有任何平衡条件限定的二叉树。

斜堆中，不能保证树的深度是对数的，但从平均概念上来说斜堆所有的操作都是对数的。

斜堆也支持归并。

2.斜堆的归并算法

斜堆的归并中，最简单的策略是将根结点值较大的堆与根结点较小的堆的右子堆进行归并。

在归并完成前，将产生的临时树的右子树上每个结点交换他们的左、右子树。

下面是最小斜堆的归并案例。

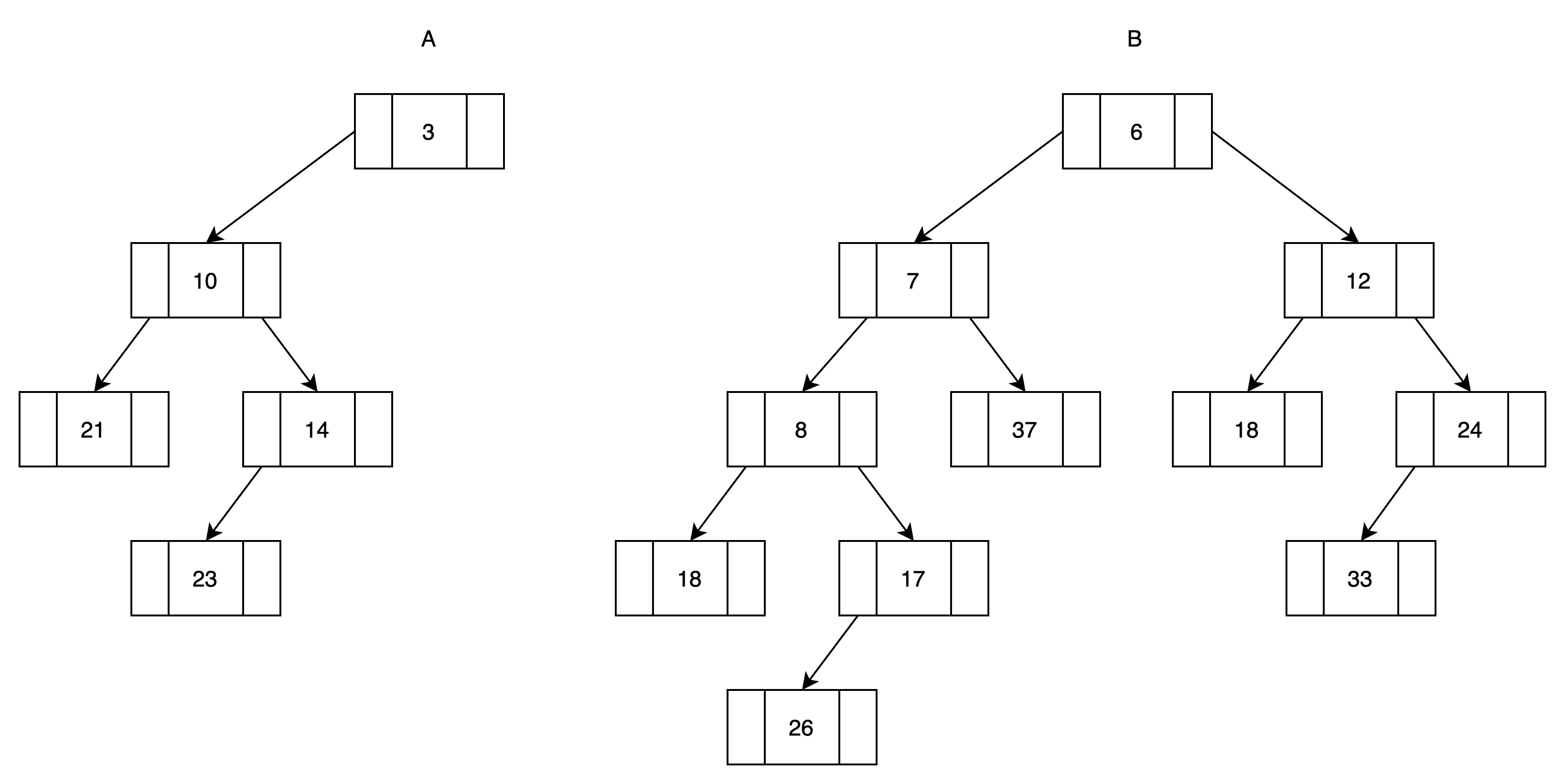
（1）准备两个堆

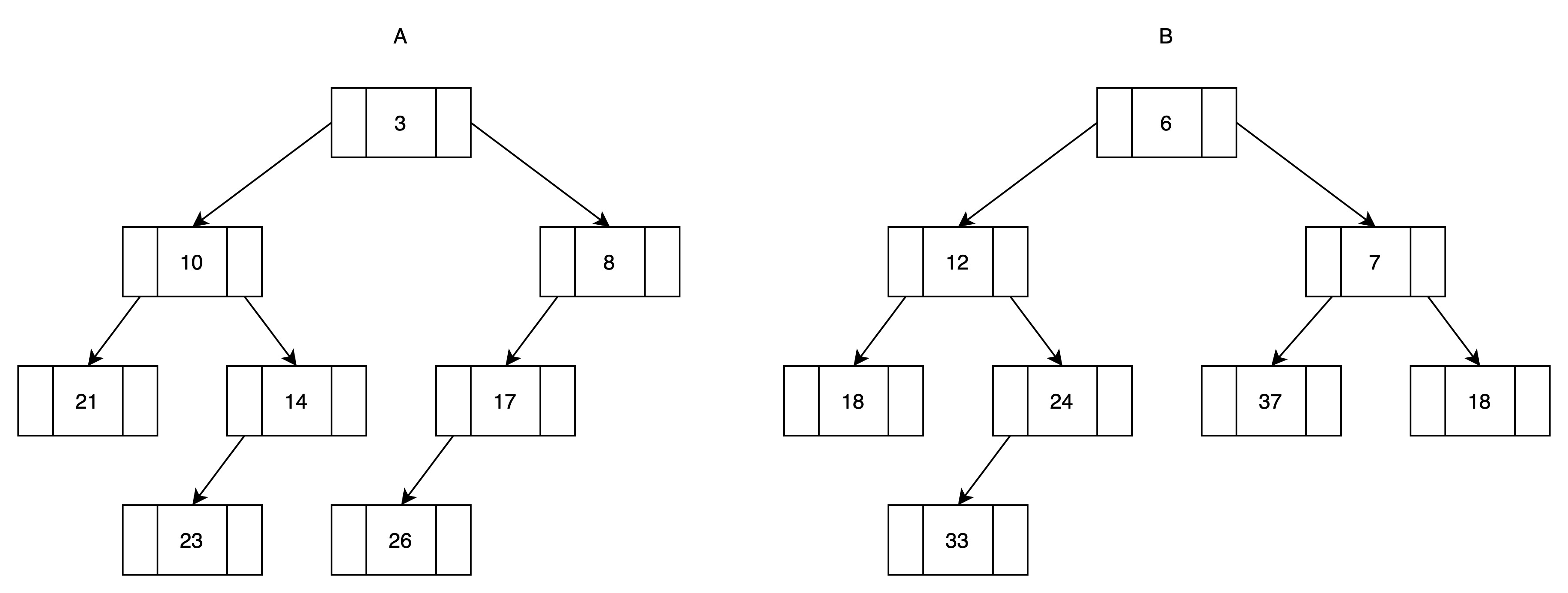
（2）将堆A和堆B进行归并

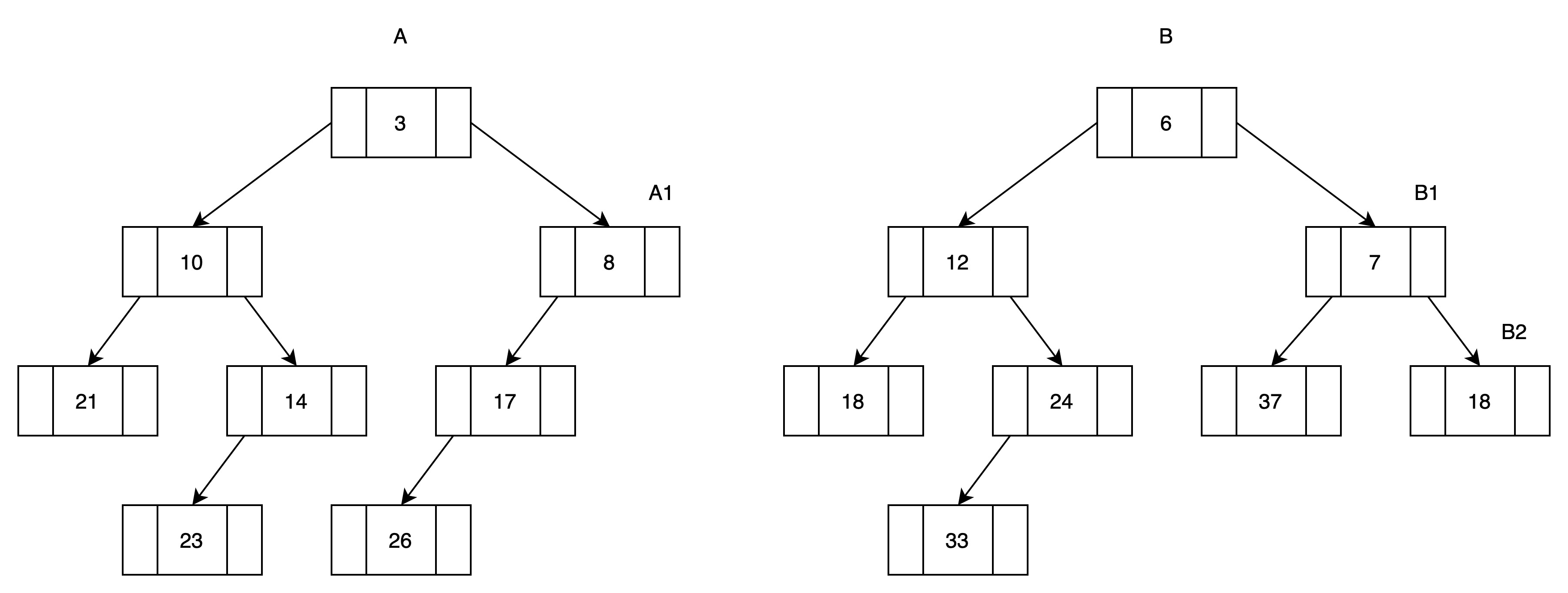
第一轮，B根结点大于A根结点，所以将A右子堆（A1）与B进行归并。归并结果作为A的右子堆。

第二轮，A1根结点大于B根结点，所以将A1与B右子堆（B1）进行归并。归并结果作为B的右子堆。

第三轮，A1根结点大于B1根结点，所以将A1与B1右子堆（B2）进行归并。归并结果作为B1的右子堆。

第四轮，A1根结点小于B2根结点，所以将A1的右子堆与B2进行归并。归并结果作为A1的右子堆。

（3）A1的右子堆为空，所以B2作为A1的右子堆，并交换A1的左右子堆

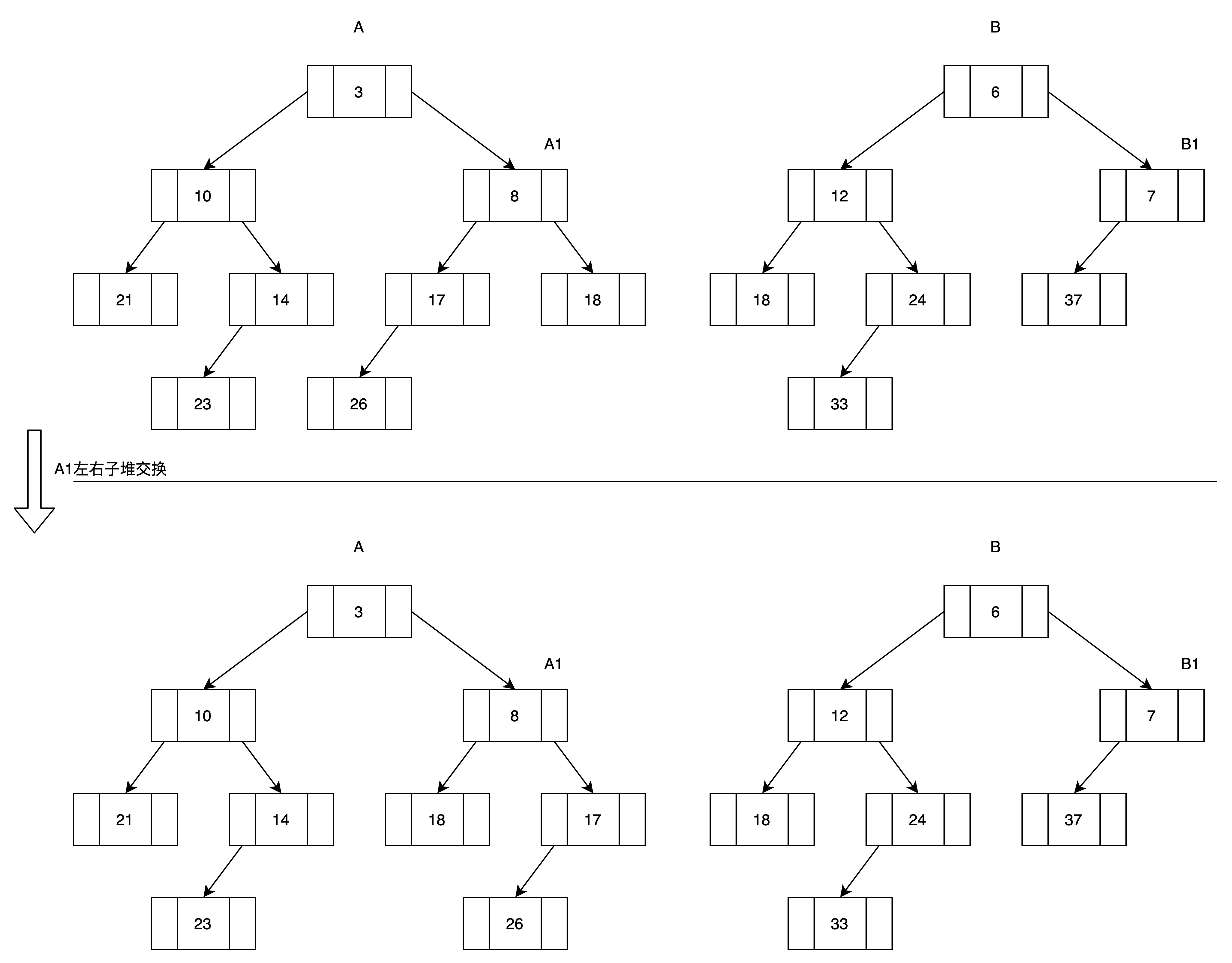
第四轮结束。

（4）B1的右子堆为空，所以将A1作为B1的右子堆，并交换B1的左右子堆。

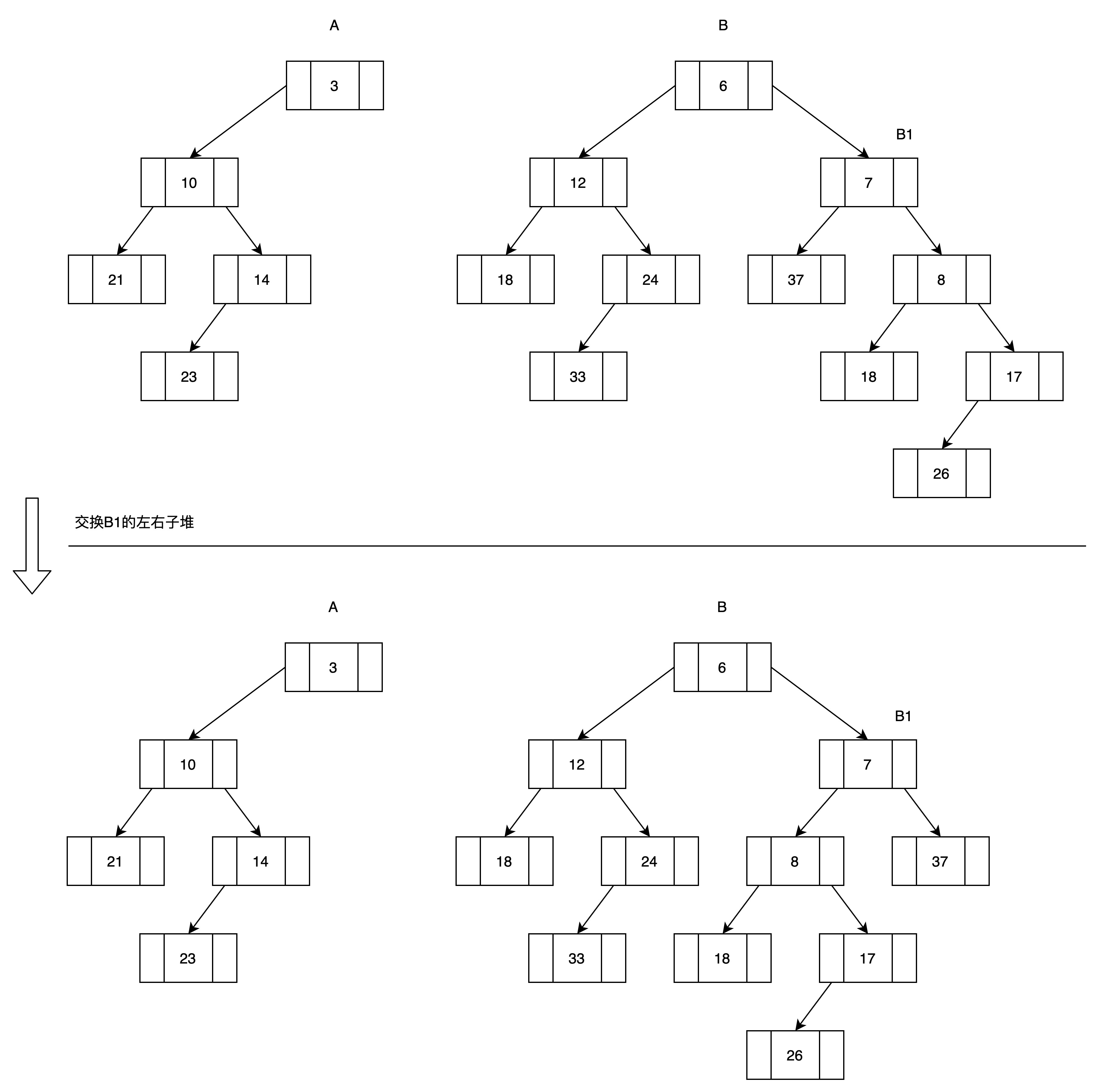
第三轮结束。

（5）A的右子堆为空，B1还是B的右子堆，但需要交换B的左右子堆。

第二轮结束。

（6）A的右子堆为空，B作为A的右子堆，并交换A的左右子堆。

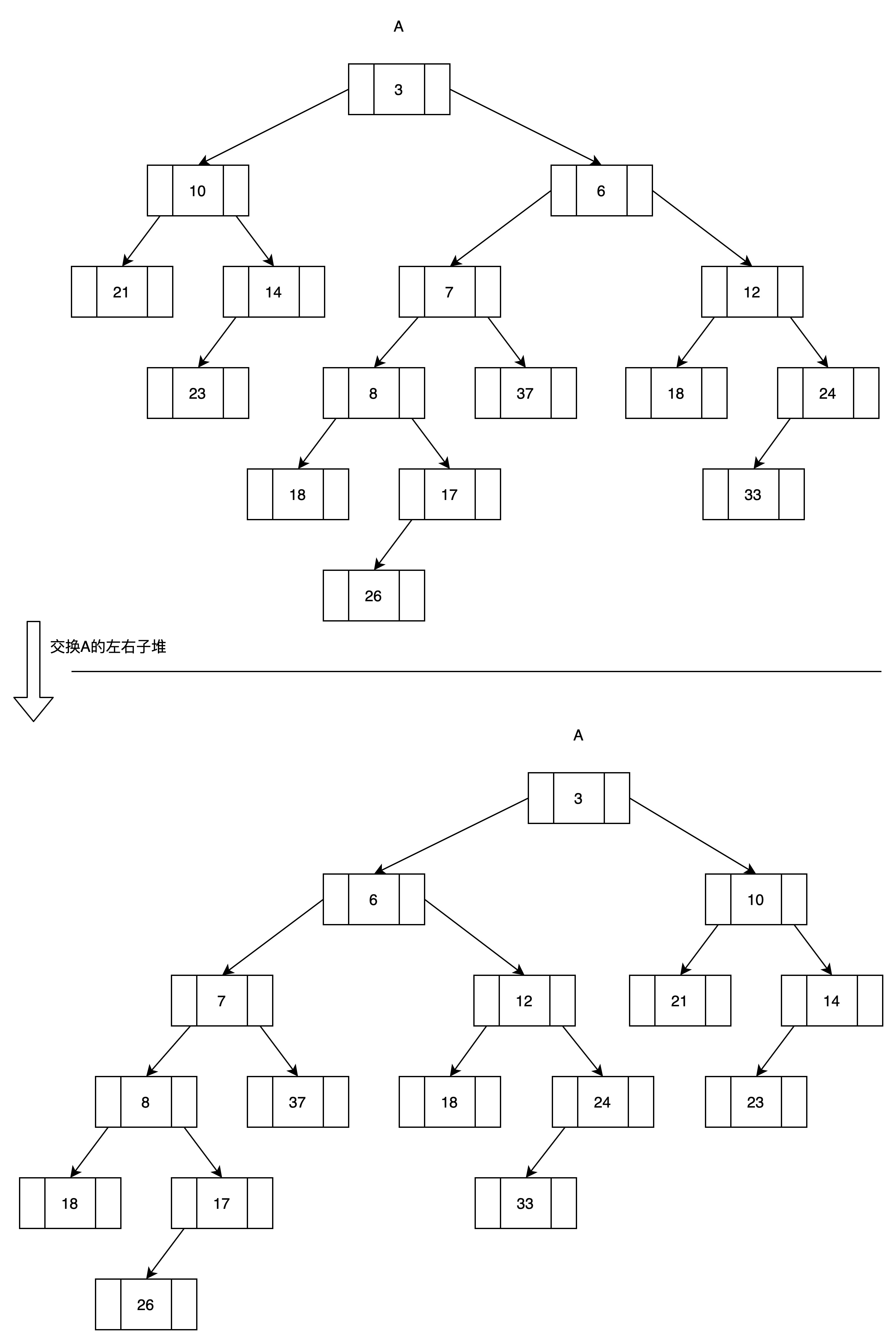
第一轮结束。

此时得到一棵树，归并结束。