二叉堆能有效支持优先级队列的入队和出队操作，但不能支持两个优先级队列的归并。能支持优先级队列归并操作的数据结构称为归并优先级队列。

1.左堆概述

左堆是一种归并优先级队列。

左堆满足堆的有序性，即堆中所有结点比儿子结点都大（小）。

但左堆不满足堆的结构性，即不是完全二叉树。

1.1.左堆的定义

首先，定义npl(x)为结点x的空路径长度，表示结点x到不满两个儿子结点的子孙结点最短路径，具有0个或者1个儿子的npl为0，空结点的npm为-1。

对于堆中的每个结点x，左儿子的npl不小于右儿子的npl，这样的堆就是左堆。

所以，左堆就是向左倾斜的堆。

下图就是一个左堆，结点值为npl

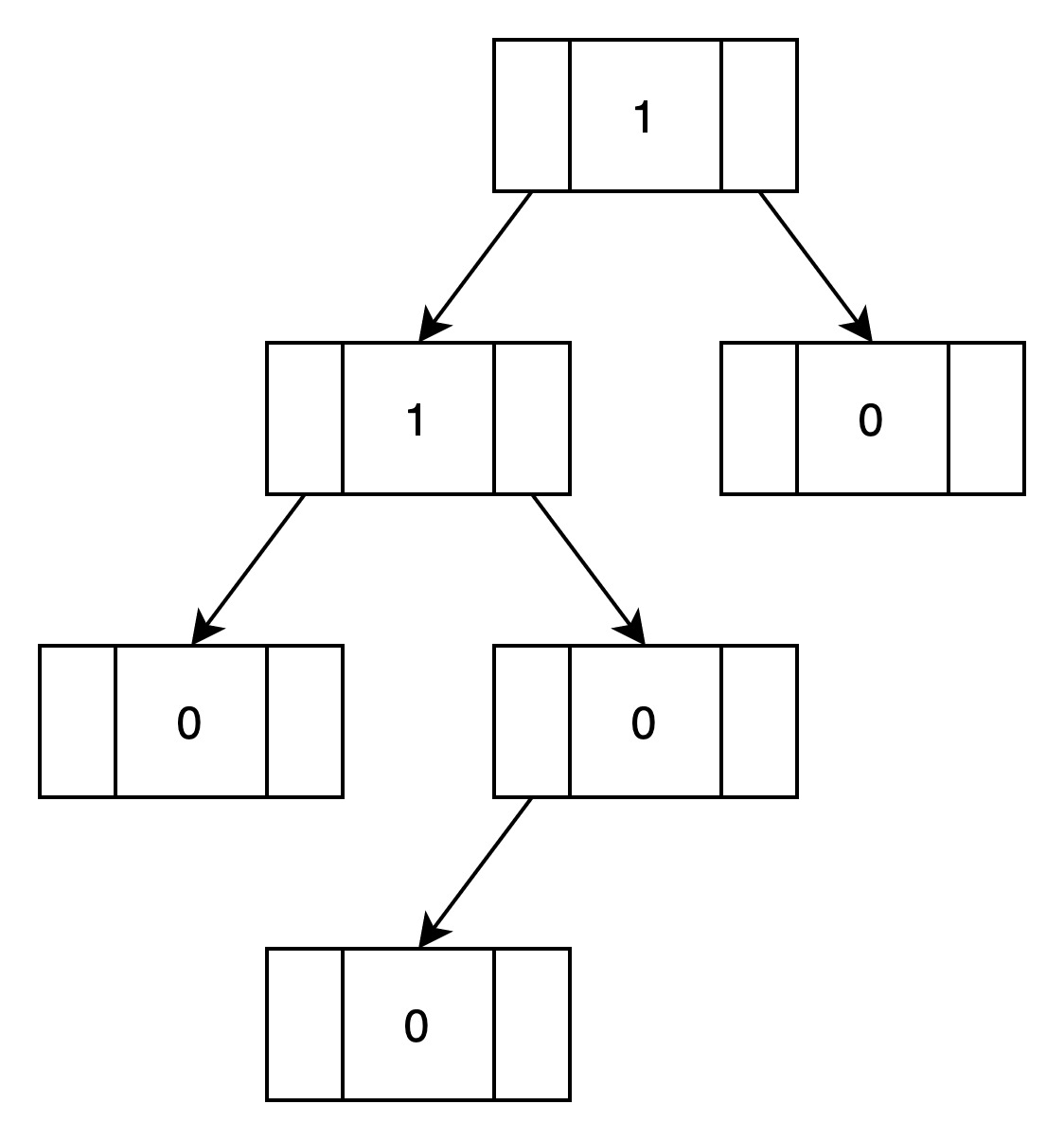
所有结点的左儿子npm都不小于右儿子的npl

下图不是一个左堆，因为红色结点的左儿子npl为0，右儿子的npl为1，不满足左堆的条件。

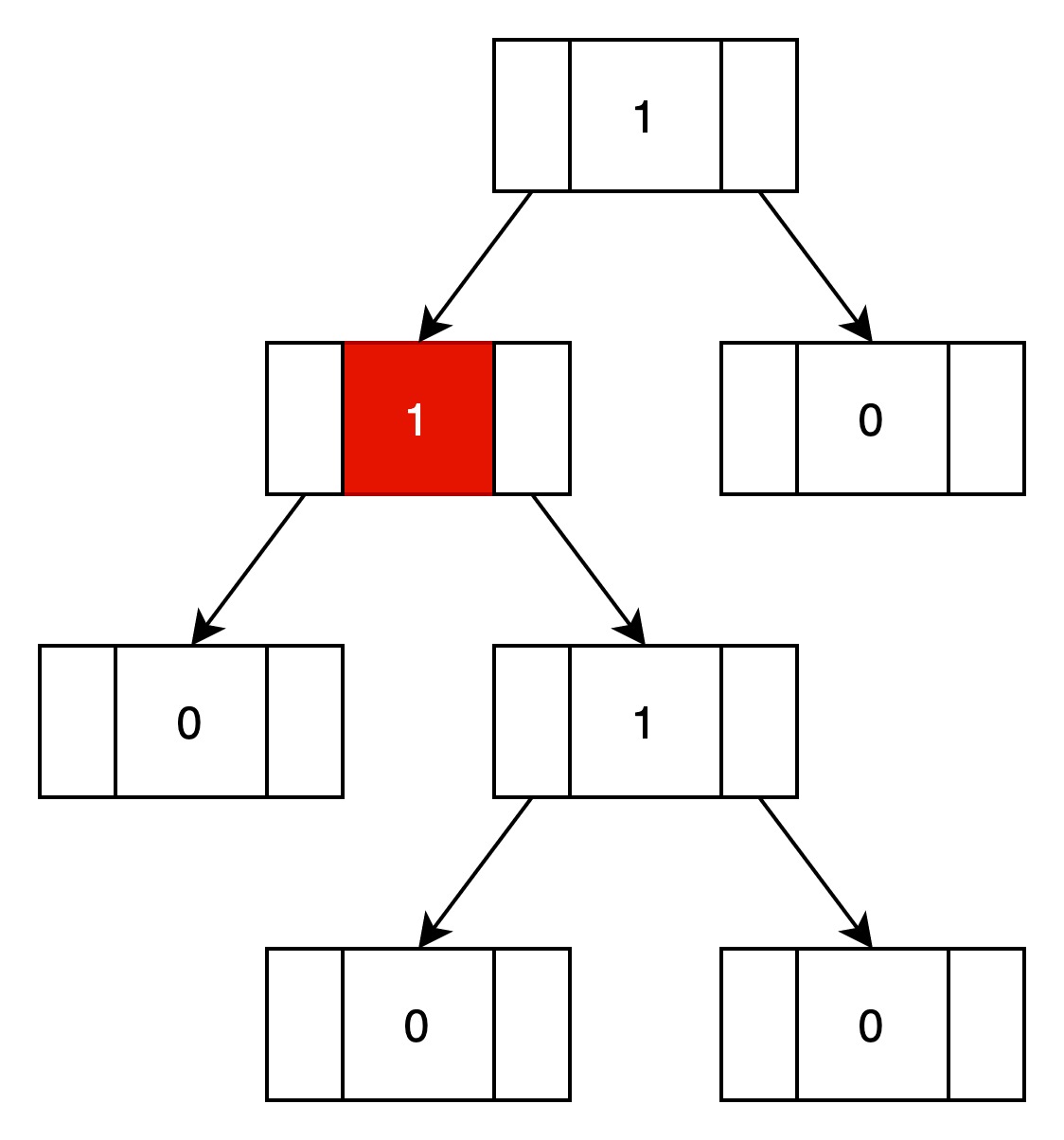
在视觉上，上图的堆也没有向左倾斜。

左堆中的每个结点需要保存元素值和结点的npl值。

左堆最主要的操作是归并。由于左堆堆平衡性的要求不高，是一个左高右低的树。所以归并就是往根结点的右子堆进行插入。

左堆的插入采用递归算法，步骤如下：

（1）将根结点稍大的堆A与另一个堆B的右子树归并，归并后的堆作为B的右子树

（2）如果产生的堆违反了左堆的定义，则交换左、右子堆

（3）递归的终止条件是：当某个子堆为空时，另一个堆就是归并的结果。

下面通过案例解释归并过程，堆为最小化堆。

（1）下面是两个待归并的左堆

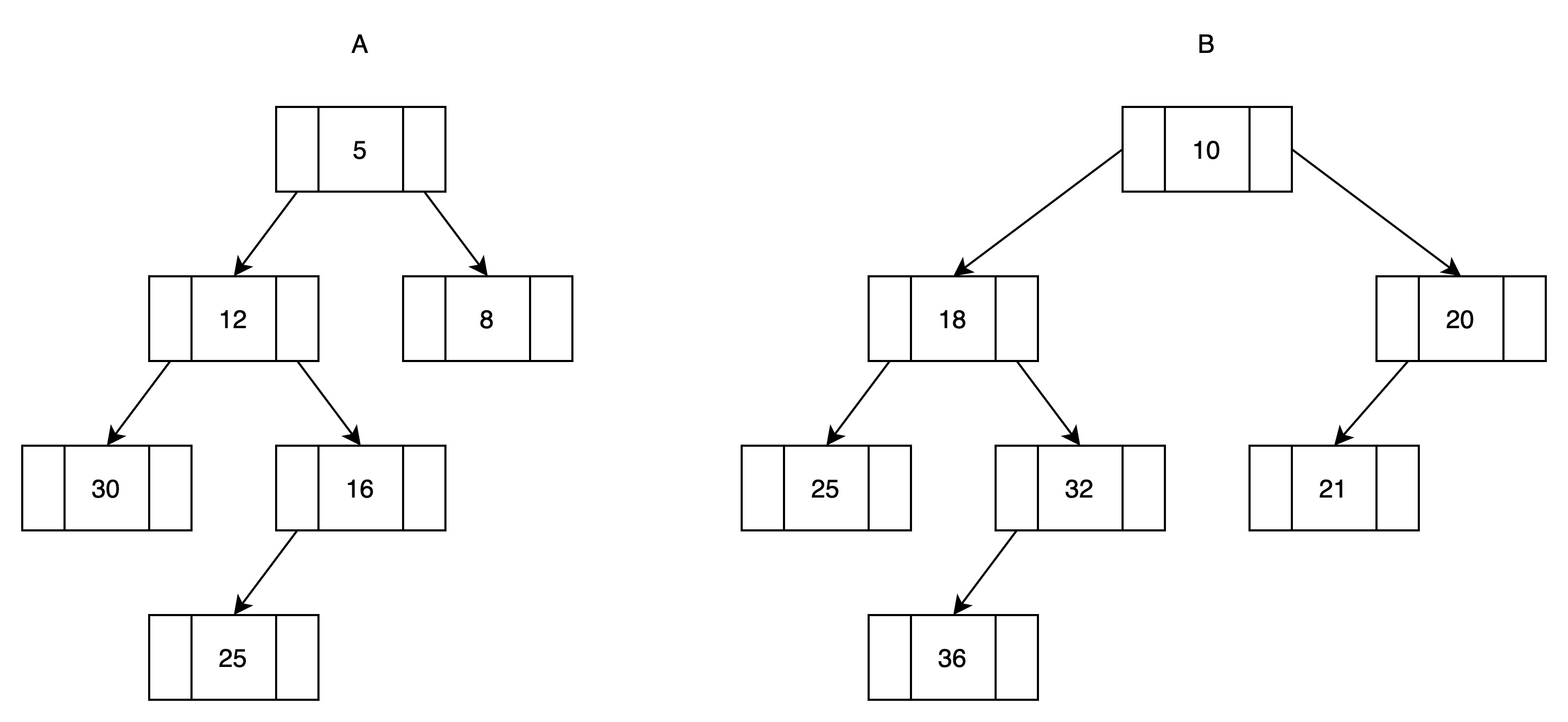
（2）将根结点稍大的堆（B）与另一个堆（A）的右子树（C）归并，

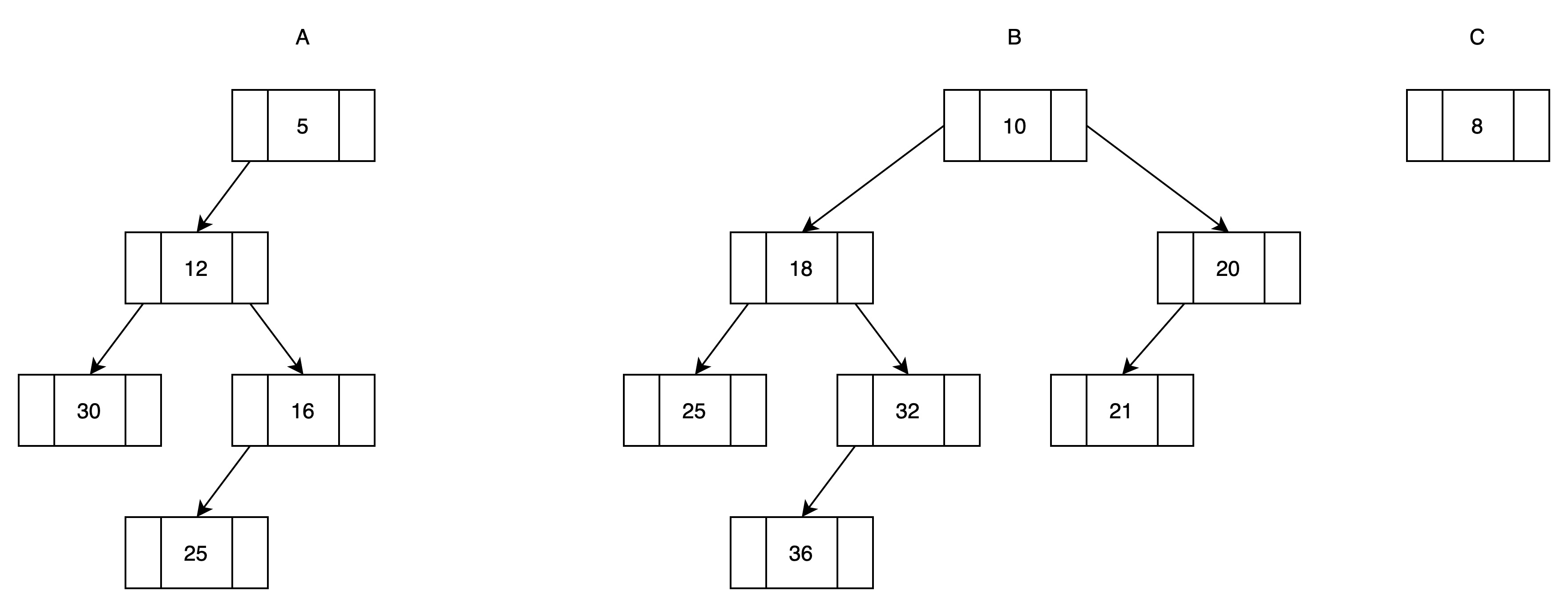
（3）将根结点稍大的堆（B）与另一个堆（C）的右子树归并。C的右子树为空，所以返回的是B，即B作为C的右子树。

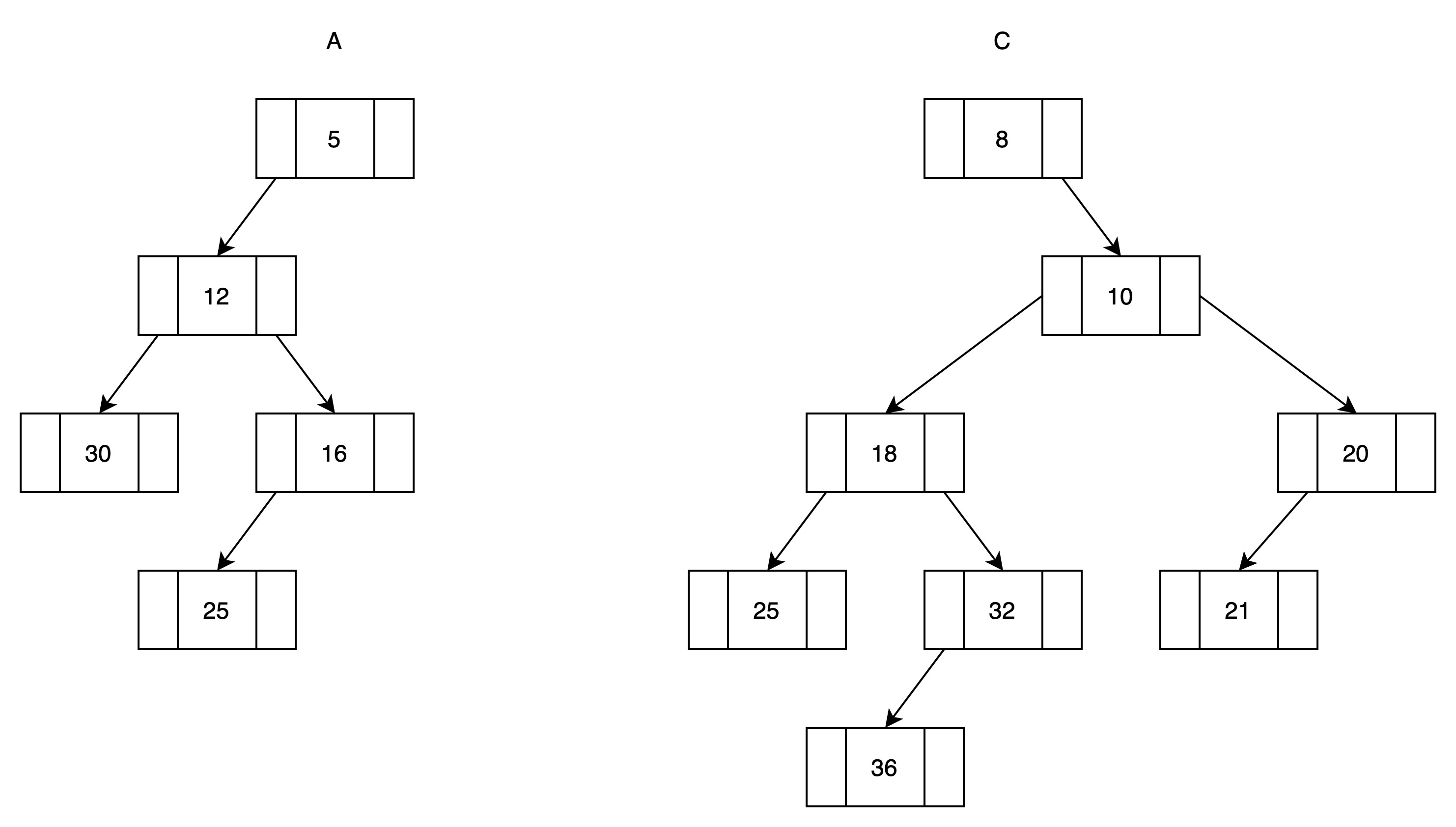
（4）此时堆C违反了左堆的定义，将C的左右子树交换

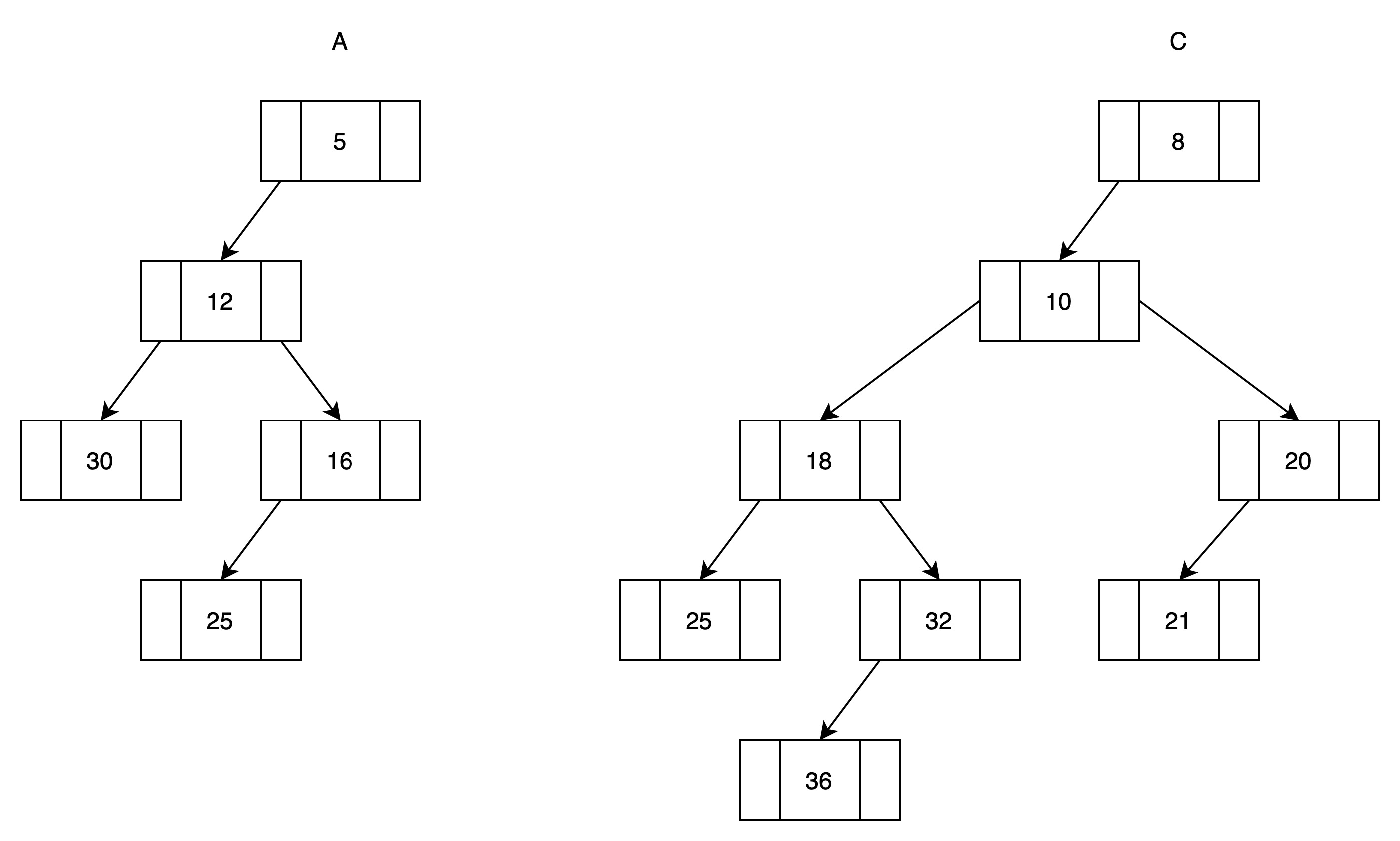
（5）C是A的右子树

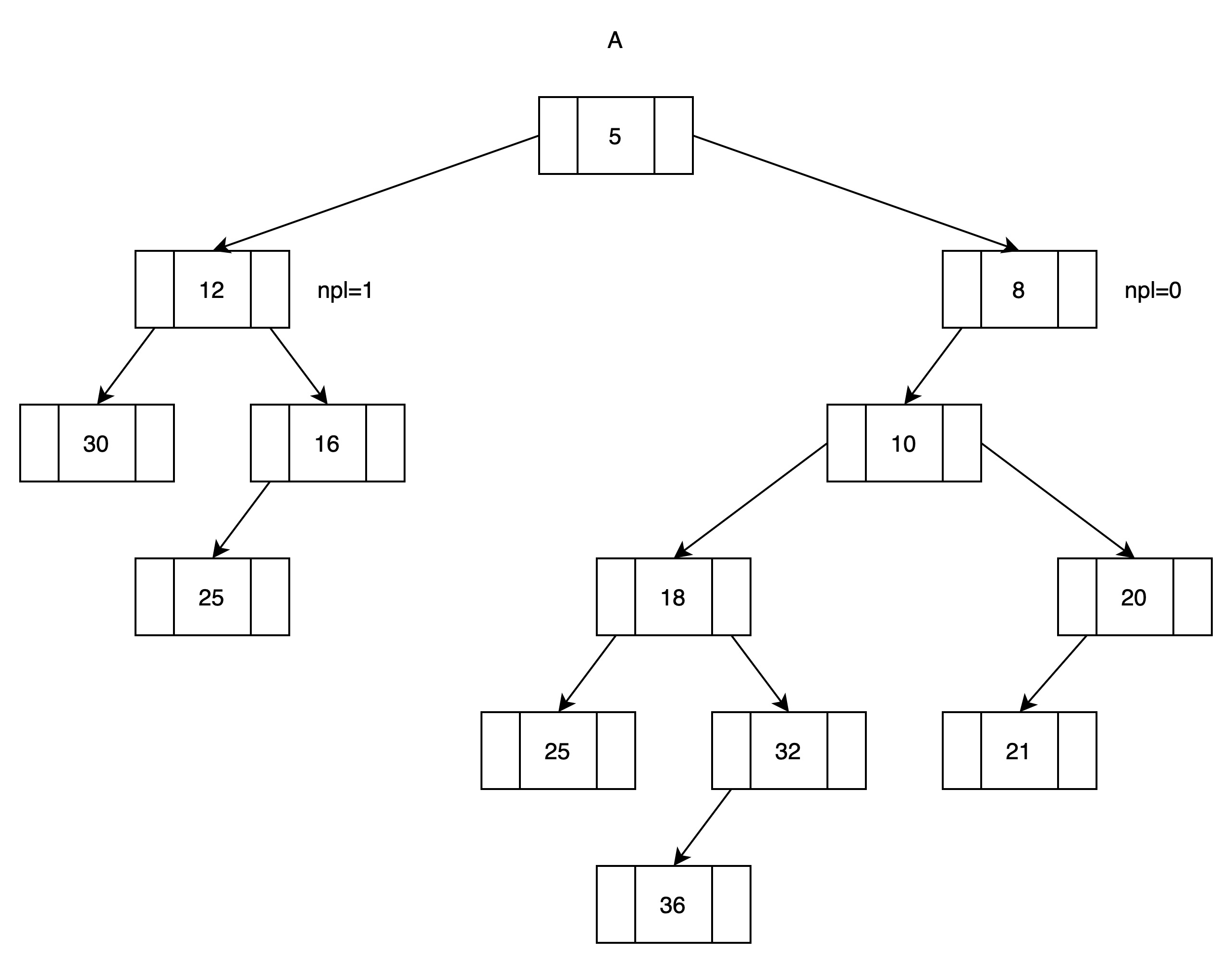
A的左儿子npl大于右儿子npl，满足左堆定义。

至此，归并结束，得到最终归并后的堆。

左堆除了归并运算，也具备普通队列的出队和入队操作，这两个操作都需要以归并操作为基础。

左堆的归并、enQueue和deQueue三个操作的时间复杂度为O(logN)

入队可以看成是原堆与单结点的堆的归并，执行归并操作即可。

出队可以看成是原堆左右两个子堆的归并，执行归并操作即可。