1.二叉堆概述

二叉堆是一种优先级队列。

1.1.优先级队列

优先级队列中，进入队列的结点必须具备优先级，结点优先级越高出队越早，结点优先级越低出队越晚，优先级相同者，则按照先进先出的原则处理。

优先级队列结点之间的关系由结点的优先级决定，而不是由入队的先后顺序决定的。

普通队列是以先进先出原则维护的，结点之间的关系由入队的先后顺序决定。

1.2.二叉堆定义

基于二叉树结构组织而成的优先级队列，就称为二叉堆。

二叉堆可以使入队和出队操作在最坏情况下时间复杂度为O(logN)。

1.3.二叉堆特性

结构性和有序性是二叉堆的两个基本特性。

1.3.1.结构性

二叉堆具有树形结构，是一颗完全二叉树。

1.3.2.有序性

任何结点都要小于（或大于）它的子孙结点。

2.二叉堆分类

二叉堆有两种表现形态。

2.1.最小二叉堆

当根结点是最小元素，且树中所有结点都小于它的子孙结点，则称为最小化堆。

最小化堆例如下图所示：

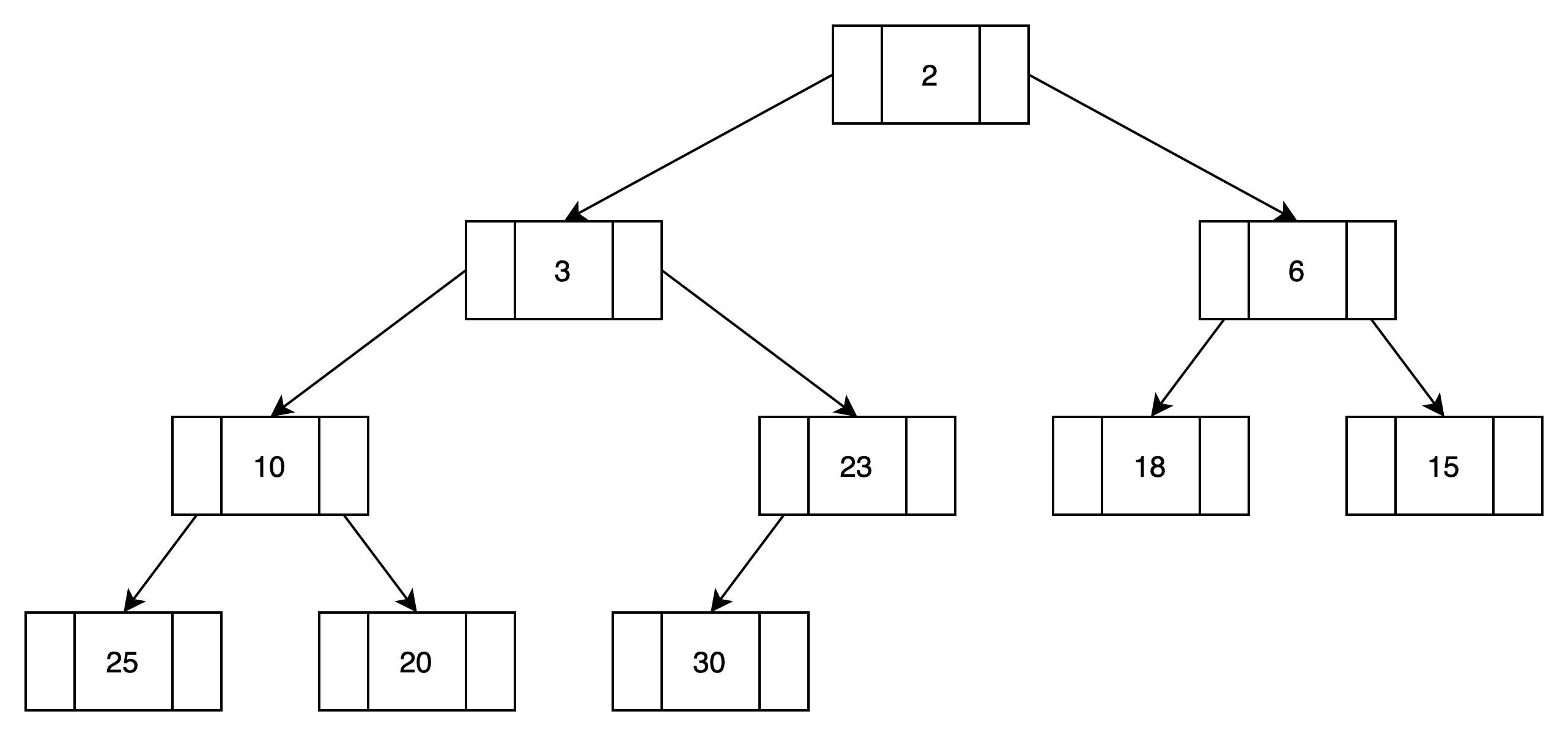
根结点为2，是树中最小的元素。

2.2.最大二叉堆

当根结点是最大元素，且树中所有结点都大于它的子孙结点，则称为最大化堆。

最大化堆例如下图所示：

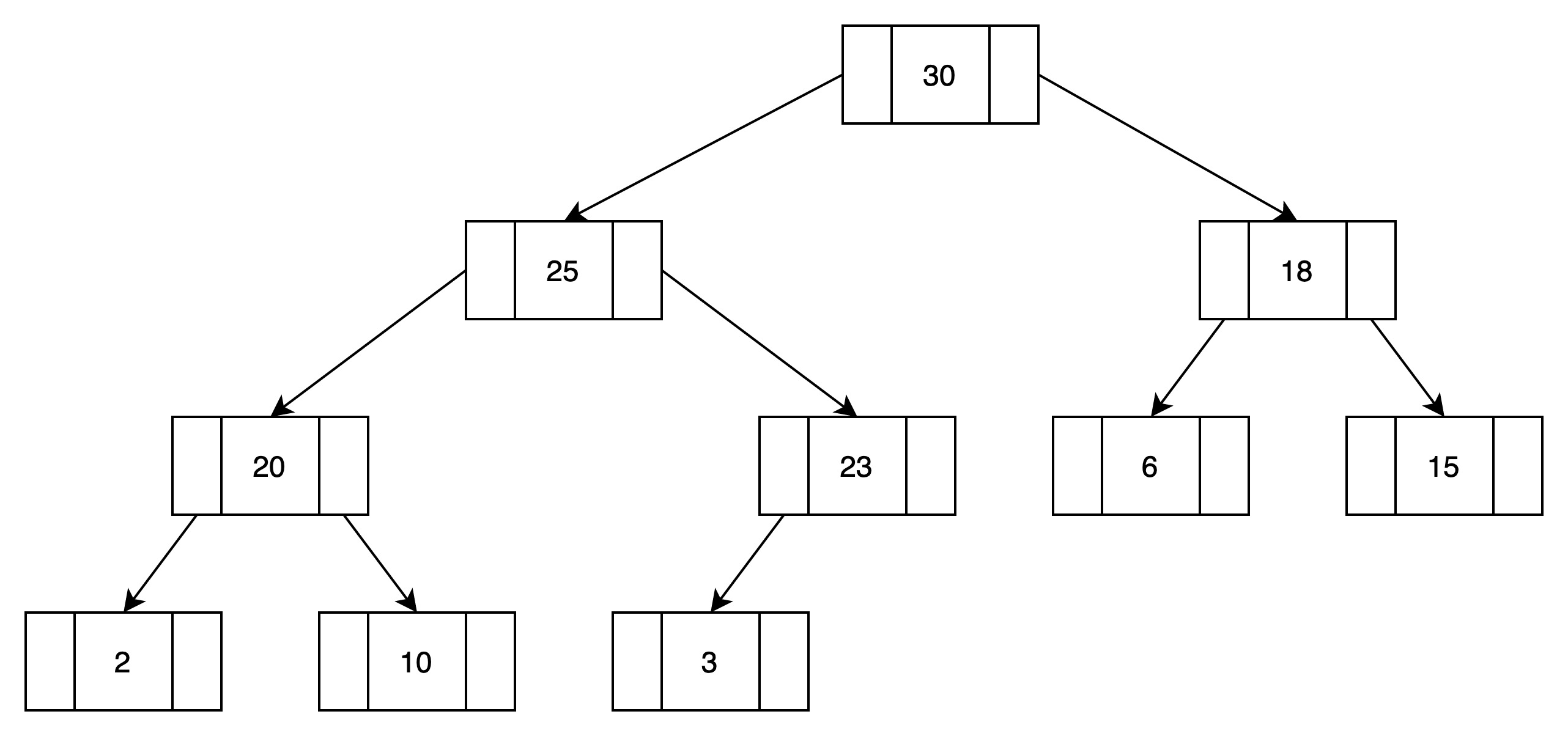
根结点为30，是树中最大的元素。

3.二叉堆运算

二叉堆支持的基本运算与普通队列相同。主要就是出堆和入堆。

3.1.deQueue

出堆是一种向下过滤的方式。

以最大化堆的出堆为例。

（1）将根结点30出堆

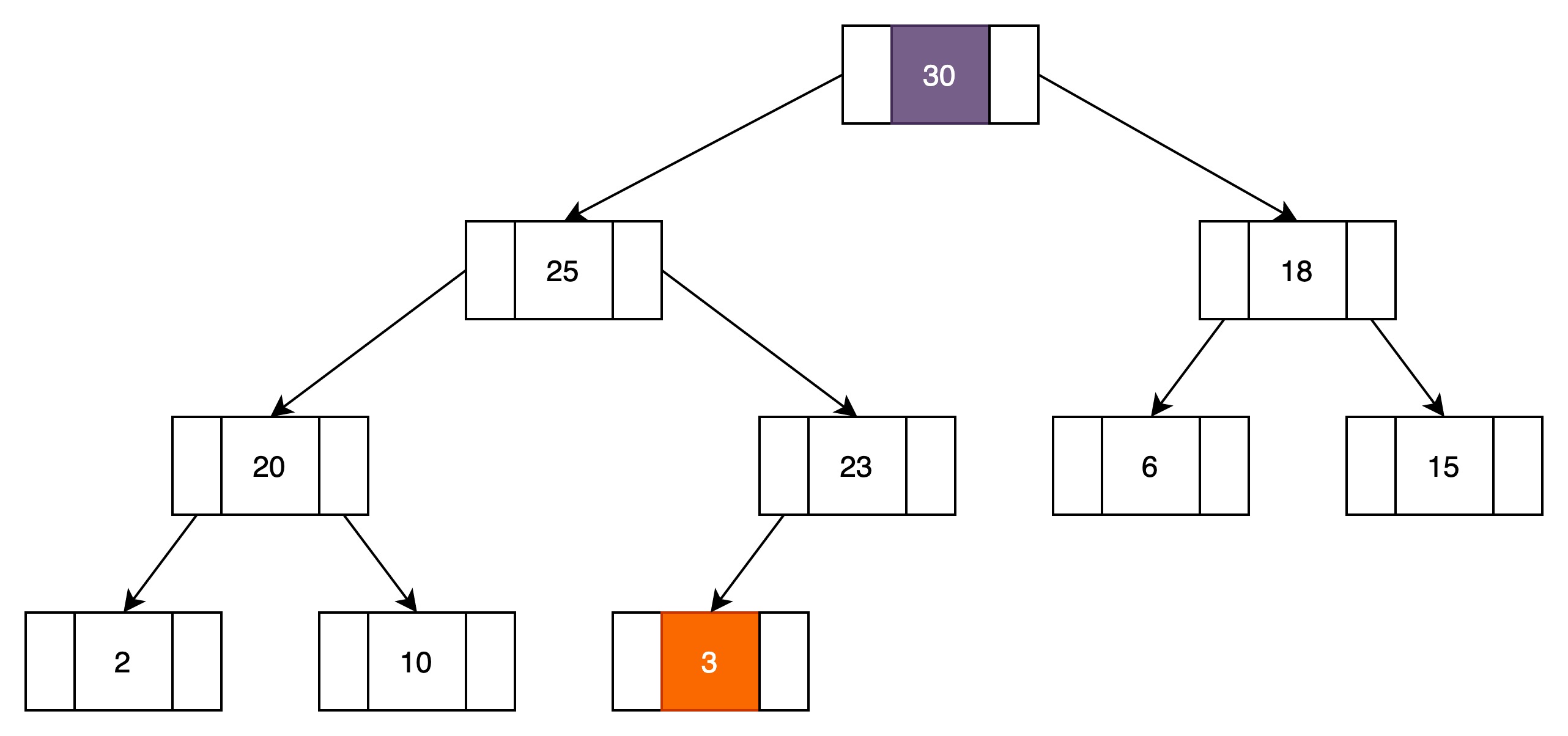
（2）将最后一个结点3移到根结点，开始向下过滤

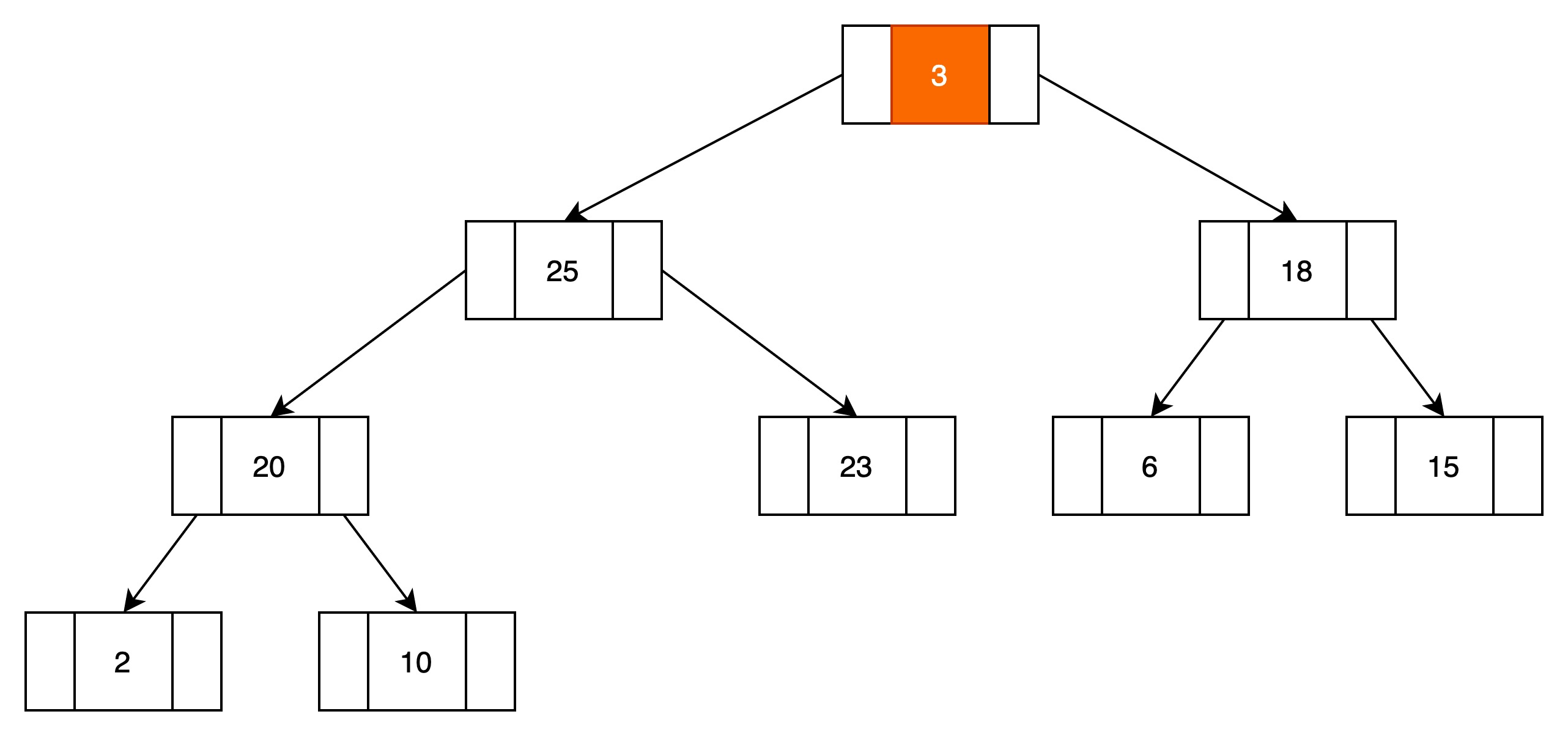
（3）当前结点与子结点比较，找到最大值，最大元素与当前结点相互进行位置转移

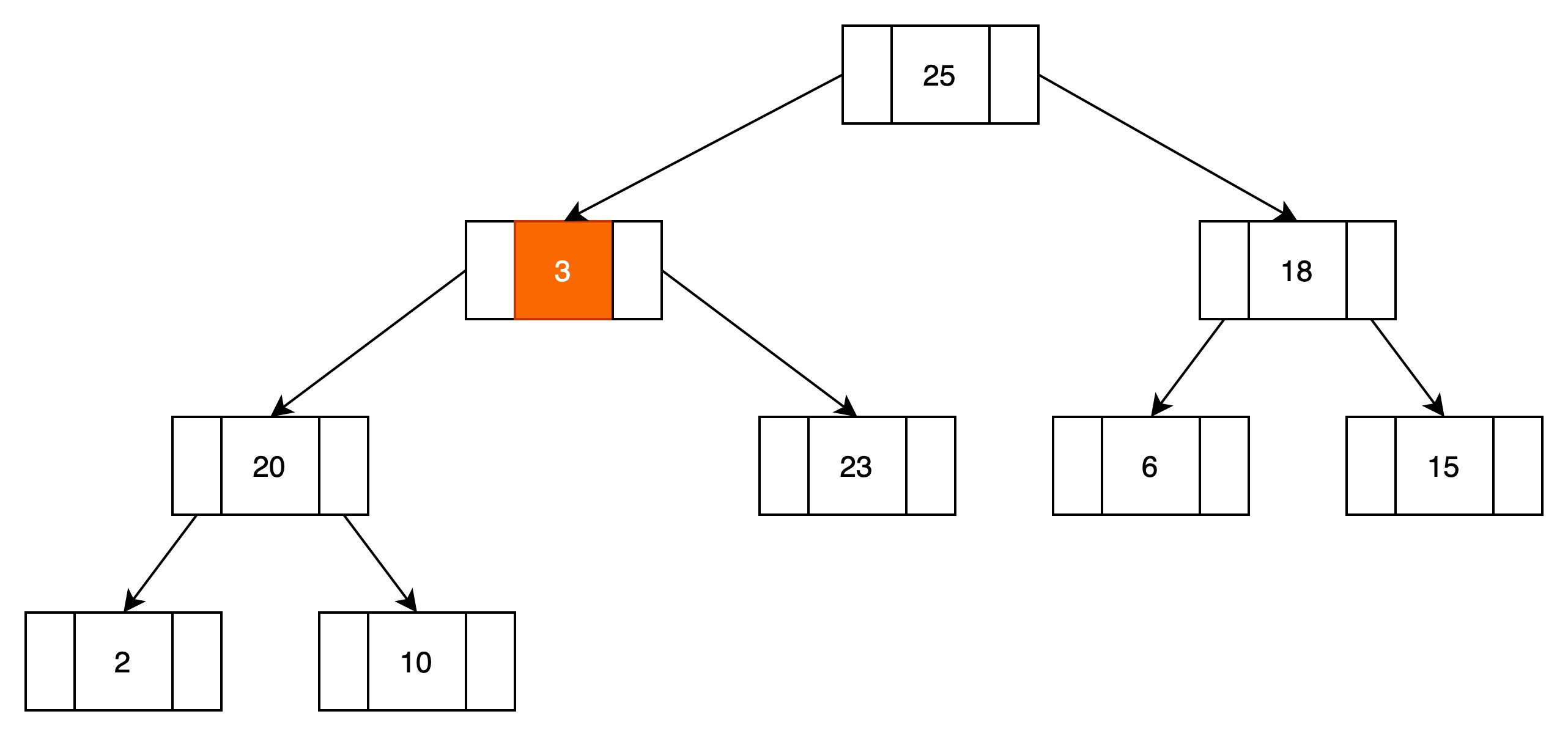
3和25进行转移

（4）当前结点与子结点比较，找到最大值，最大元素与当前结点相互进行位置转移

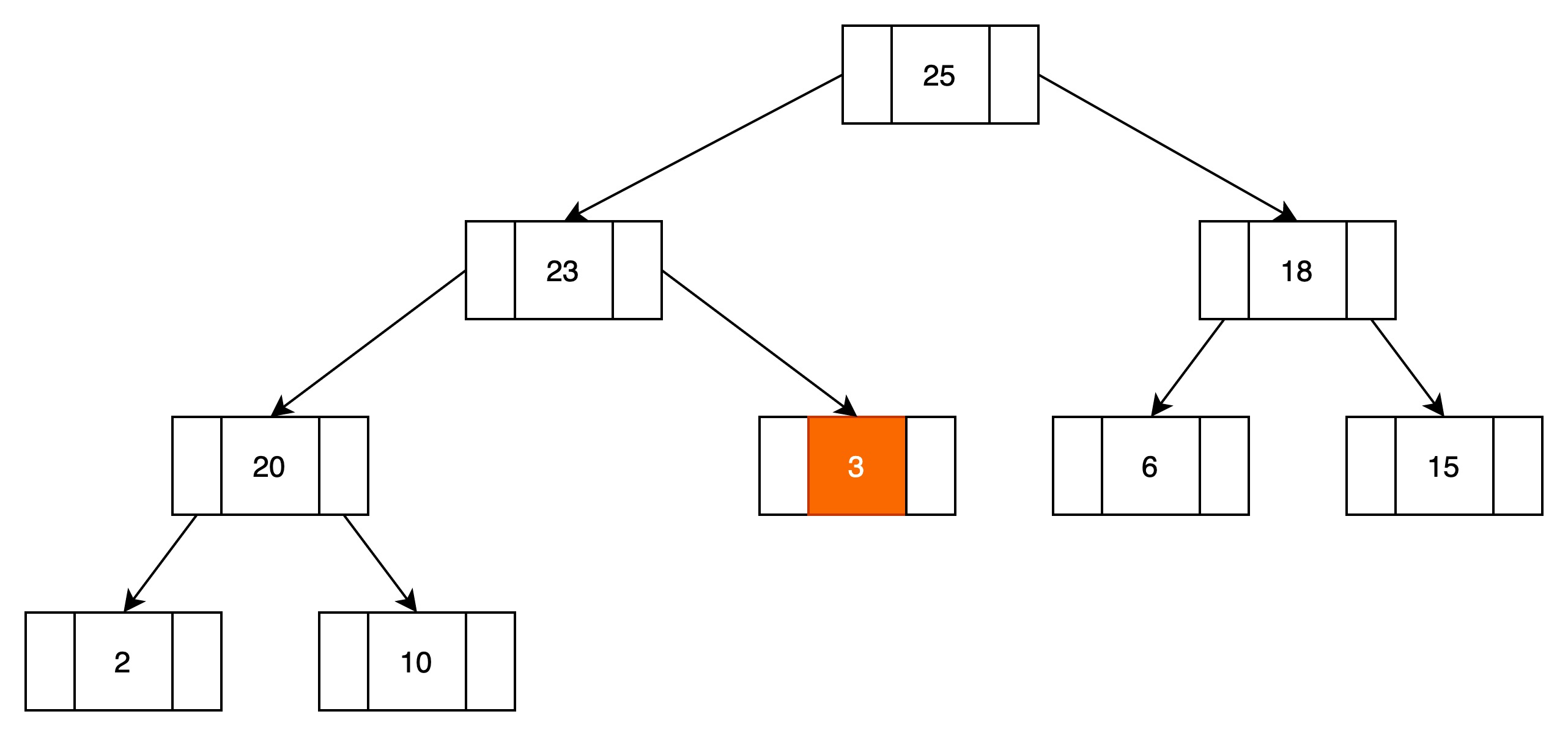
将3和23进行转移。

当前结点如果满足顺序，或者当前结点没有子结点，则循环结束，向下过滤完成。

3.2.enQueue

入堆是一种向上过滤的方式。

以最小化堆的出堆为例。

（1）新增一个元素1，放入最后的结点

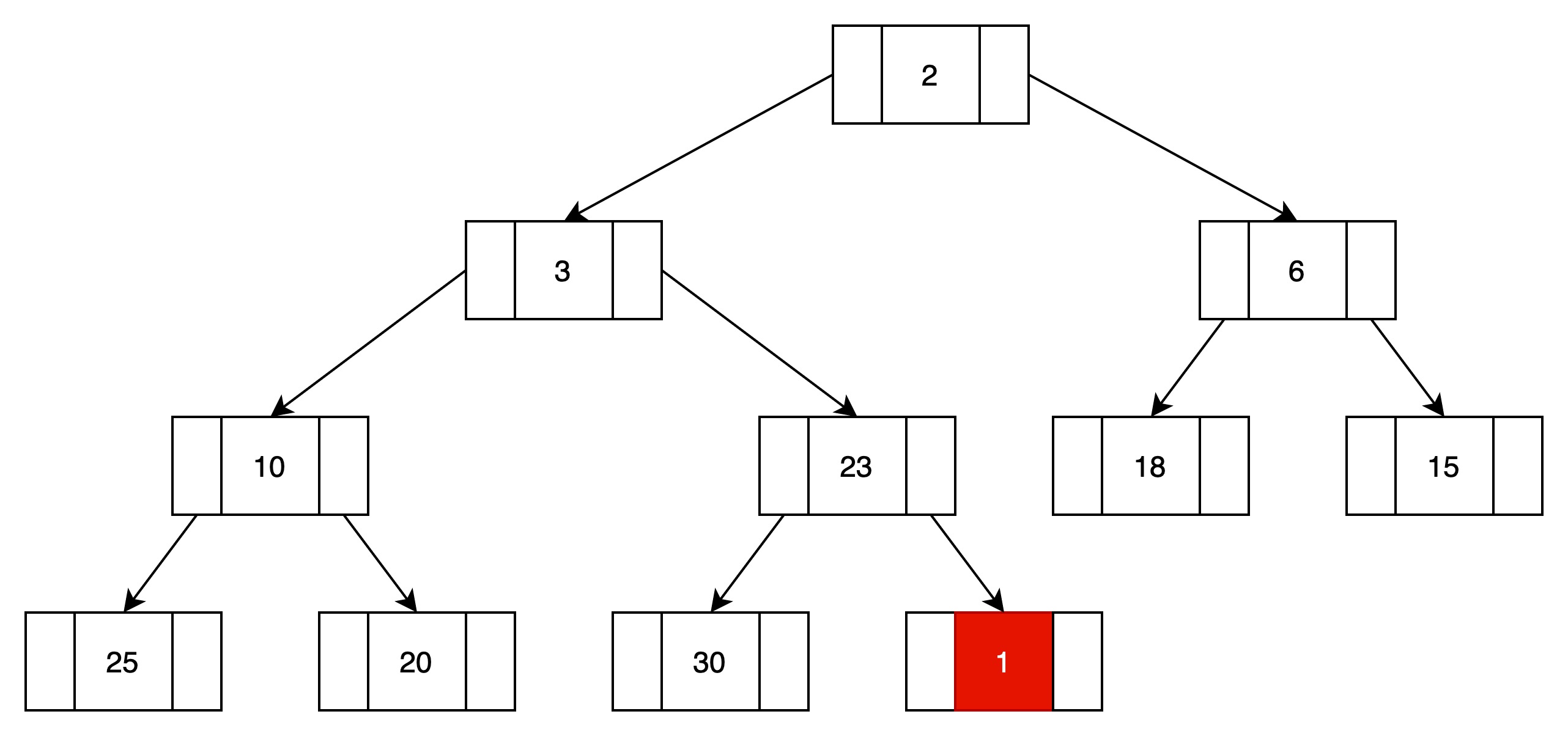
（2）向上过滤，如果父结点比当前结点小，则进行位置替换。

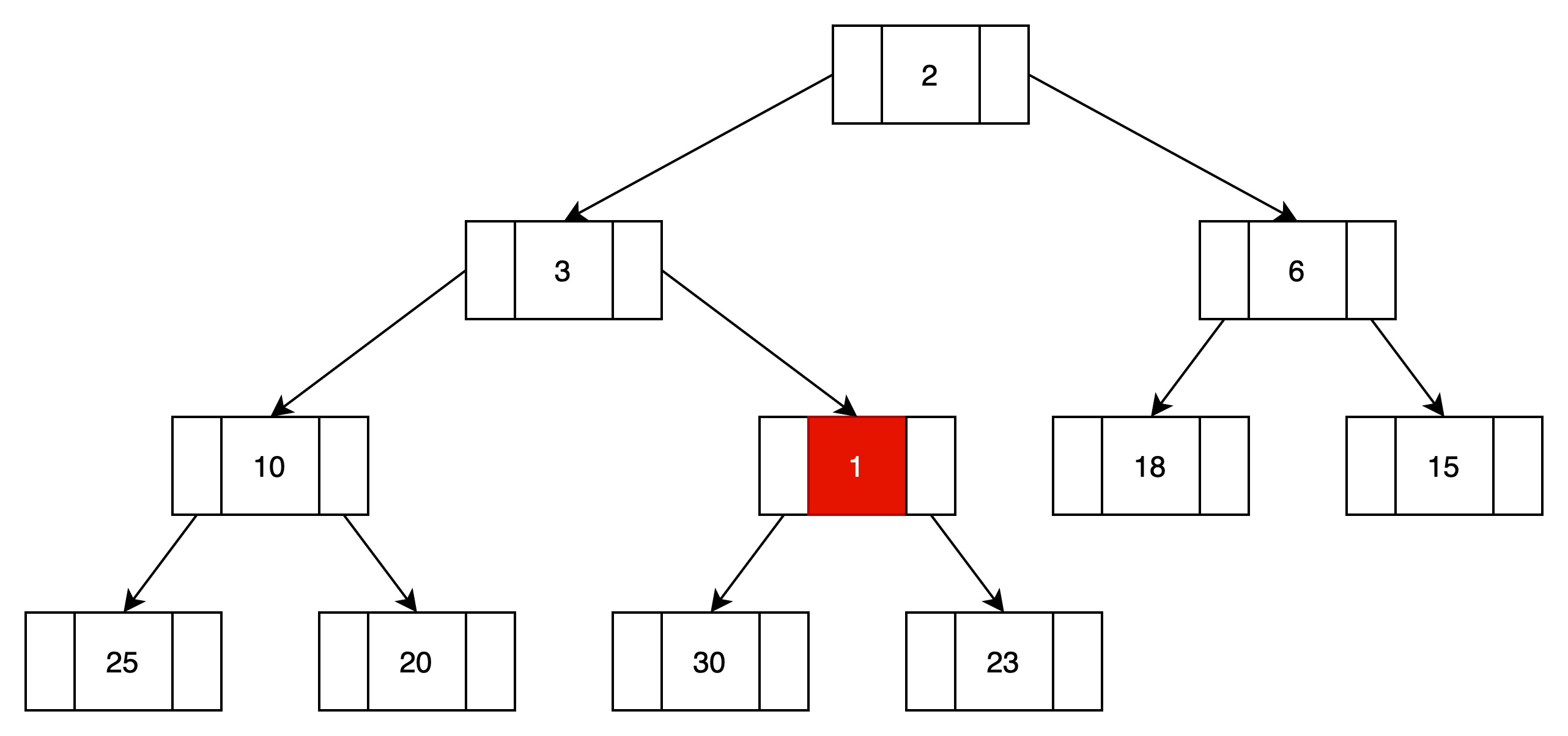
将结点1和23进行替换

（3）向上过滤，如果父结点比当前结点小，则进行位置替换。

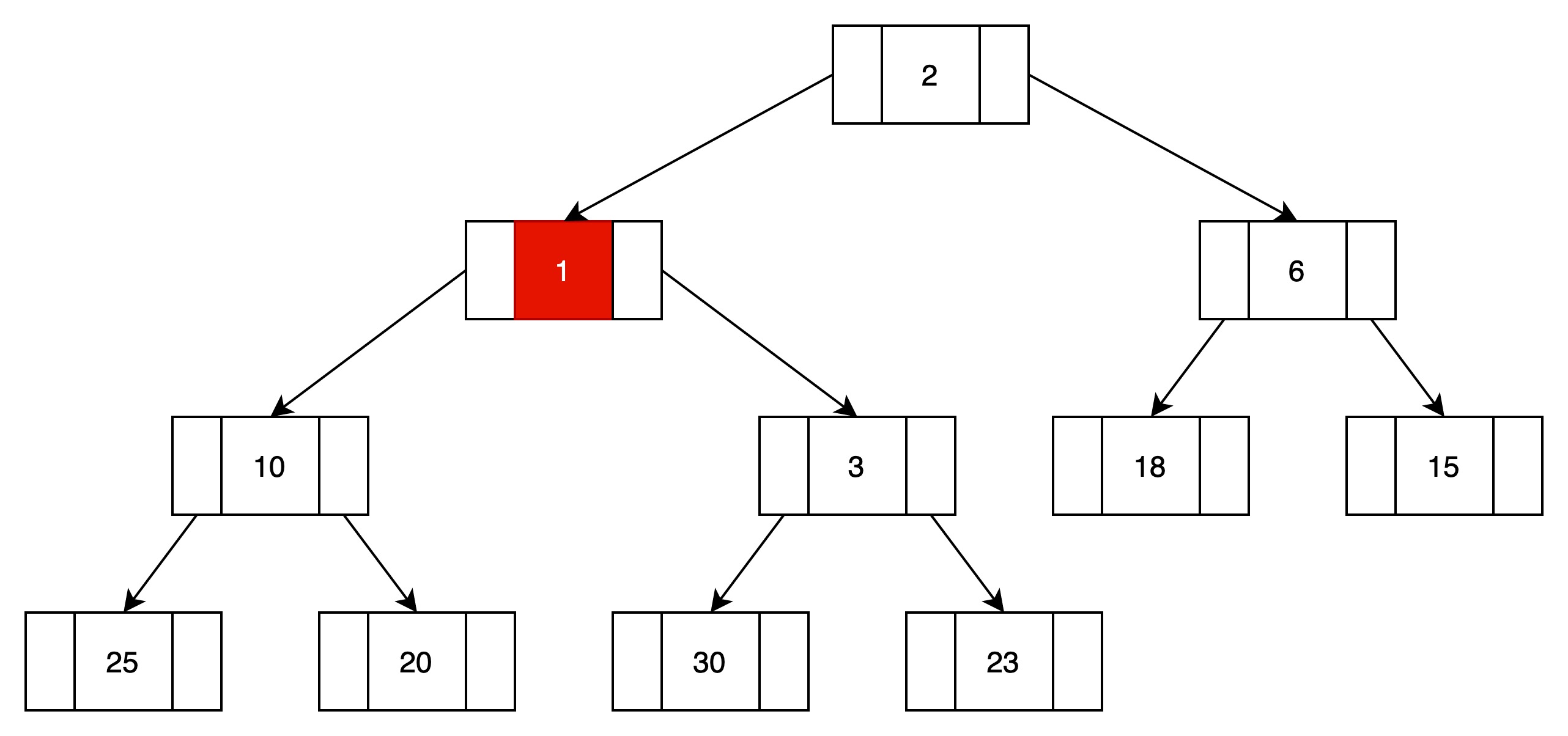
将结点1和结点3进行位置转移

（4）向上过滤，如果父结点比当前结点小，则进行位置替换。

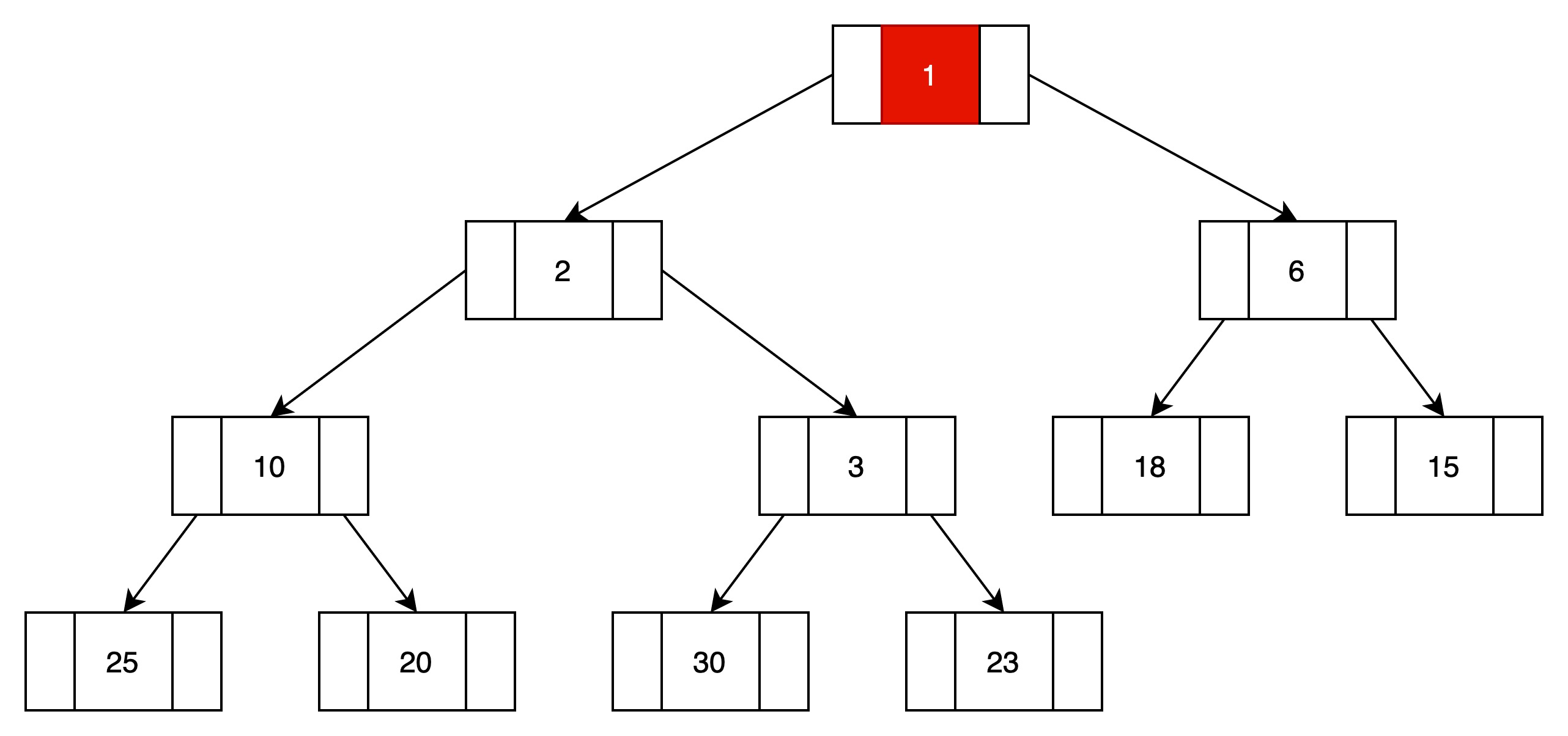
将结点1和结点2进行位置转移。

如果当前结点为根结点，或者与父结点比较后没有进行位置替换，则循环结束，向上过滤完成。