1.从二叉堆到D堆
在二叉堆中,enQueue和deQueue操作所需的时间与堆的高度相关。如果能降低堆的高度,就能进一步提高性能。
D堆就是迎合此场景而诞生的。
2.D堆结构
D堆中,每个节点有D个儿子,二叉堆就是2堆。D堆也是一颗完全D叉树。D堆满足堆的结构性和有序性。
下图是一个4堆
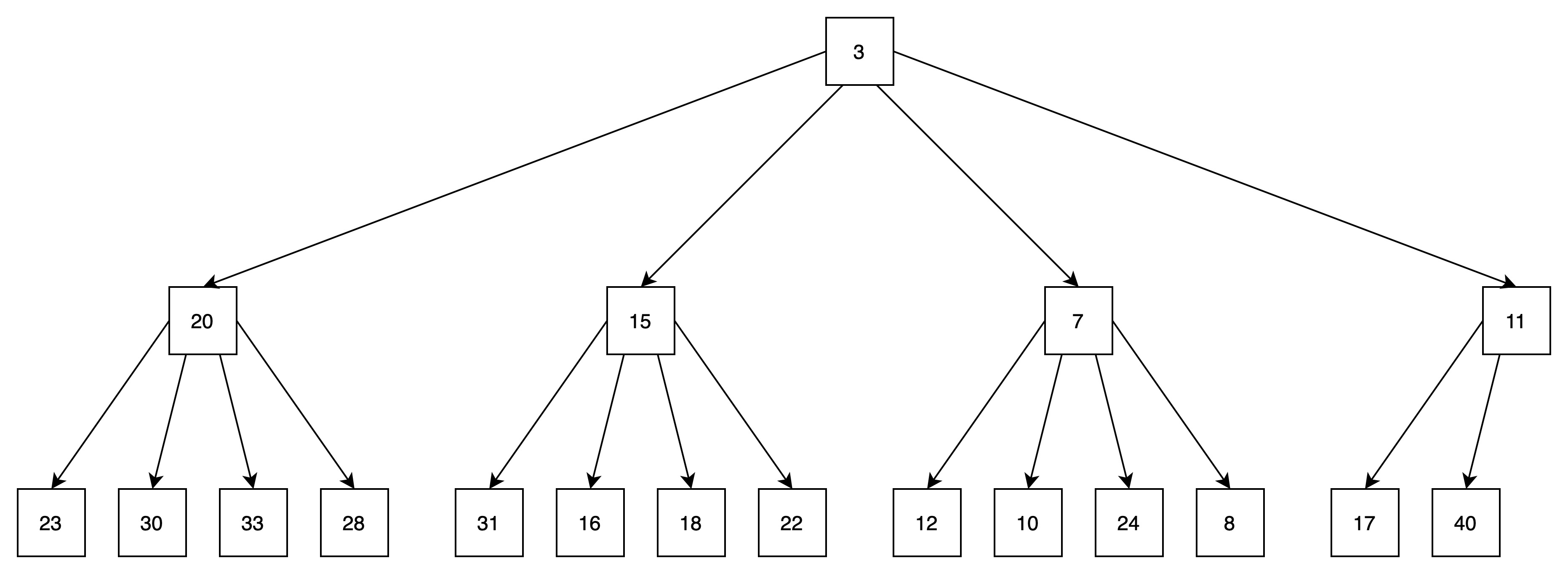
上图4堆中,元素个数为19个。
对应3层的4堆,最多可容纳(1-4^3) / (1 - 4) = 21个元素。
2.1.enQueue
入队操作时间复杂度降为O(logDN)。
下面通过最小化4堆为例说明D堆入队操作。
(1)在4堆中插入元素2
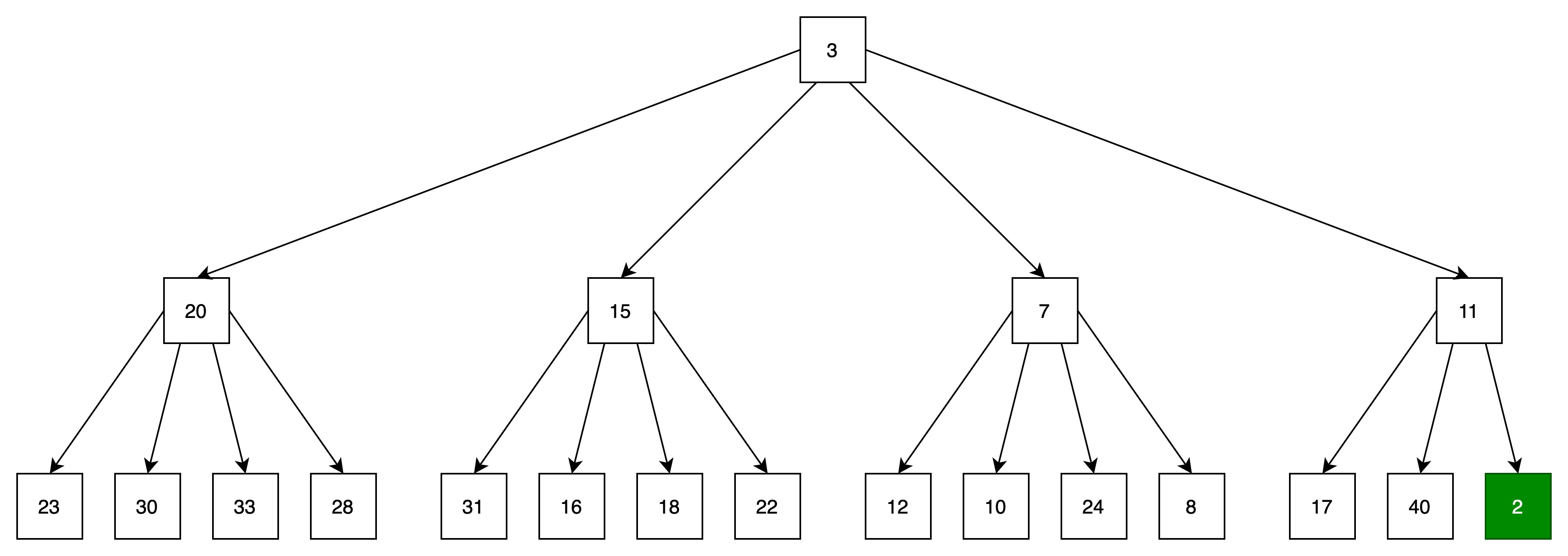
将元素2放到最后的节点
(2)向上过滤,将当前结点与父结点比较,如果当前结点比父结点小,则当前结点与父结点进行位置转移。
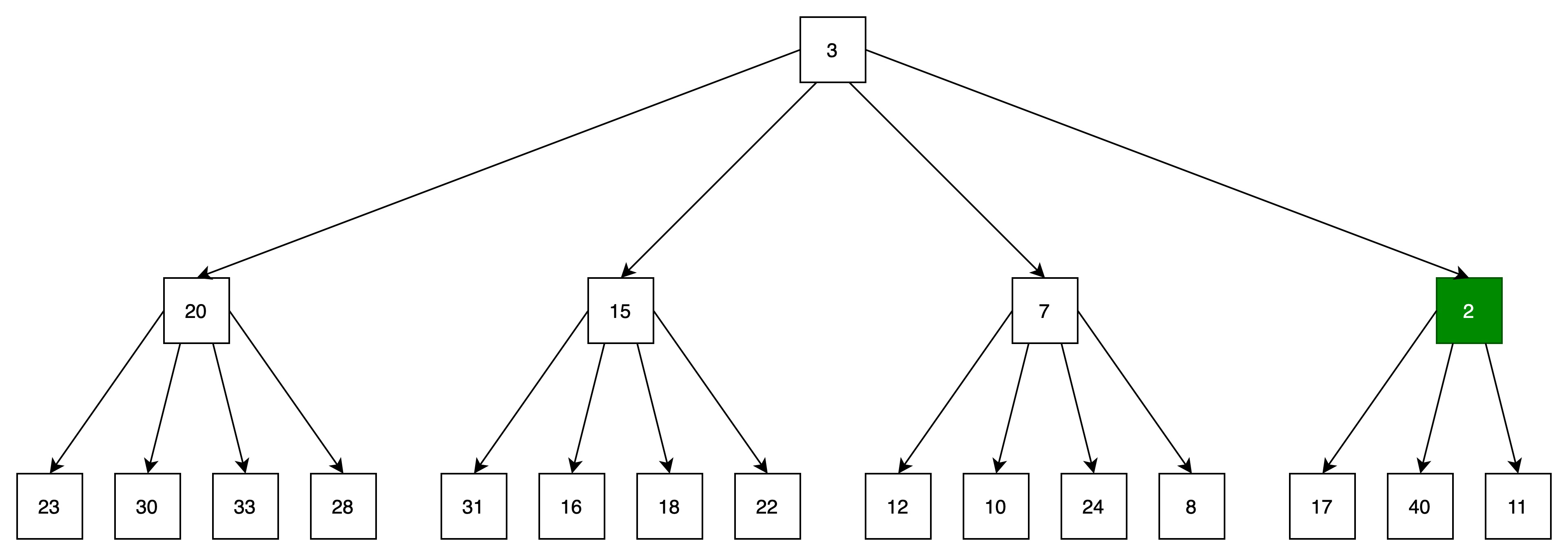
结点2与结点11进行调换。
(3)向上过滤,将当前结点与父结点比较,如果当前结点比父结点小,则当前结点与父结点进行位置转移。
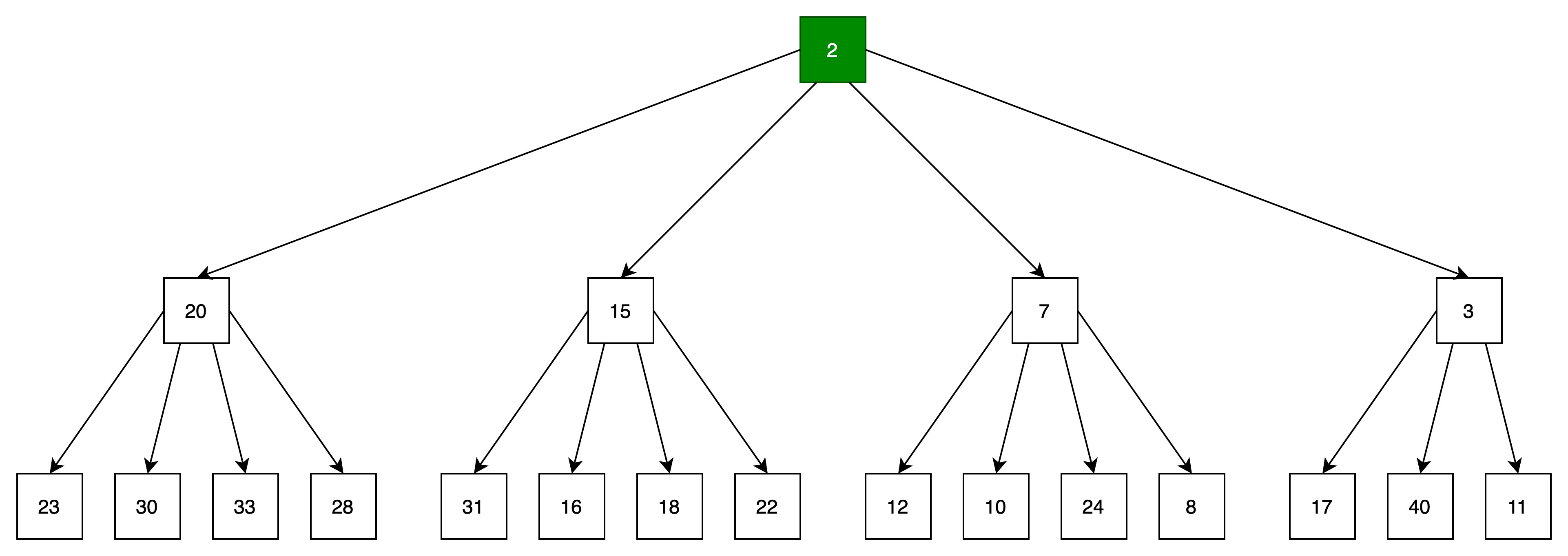
结点2与结点3进行位置转移。
当前结点与父结点关系满足堆的顺序性,或者当前结点为根结点,则向上过滤结束,完成入队操作。
2.2.deQueue
出队操作需要找到D个儿子结点中最小(大)的子结点,会涉及当前结点与所有子结点的比较,共需要进行D-1次比较。
这样出队的时间复杂度提高到O(DlogDN)。
下面通过最小化4堆为例说明D堆出队操作。
(1)构建一个4堆,将队头元素出队
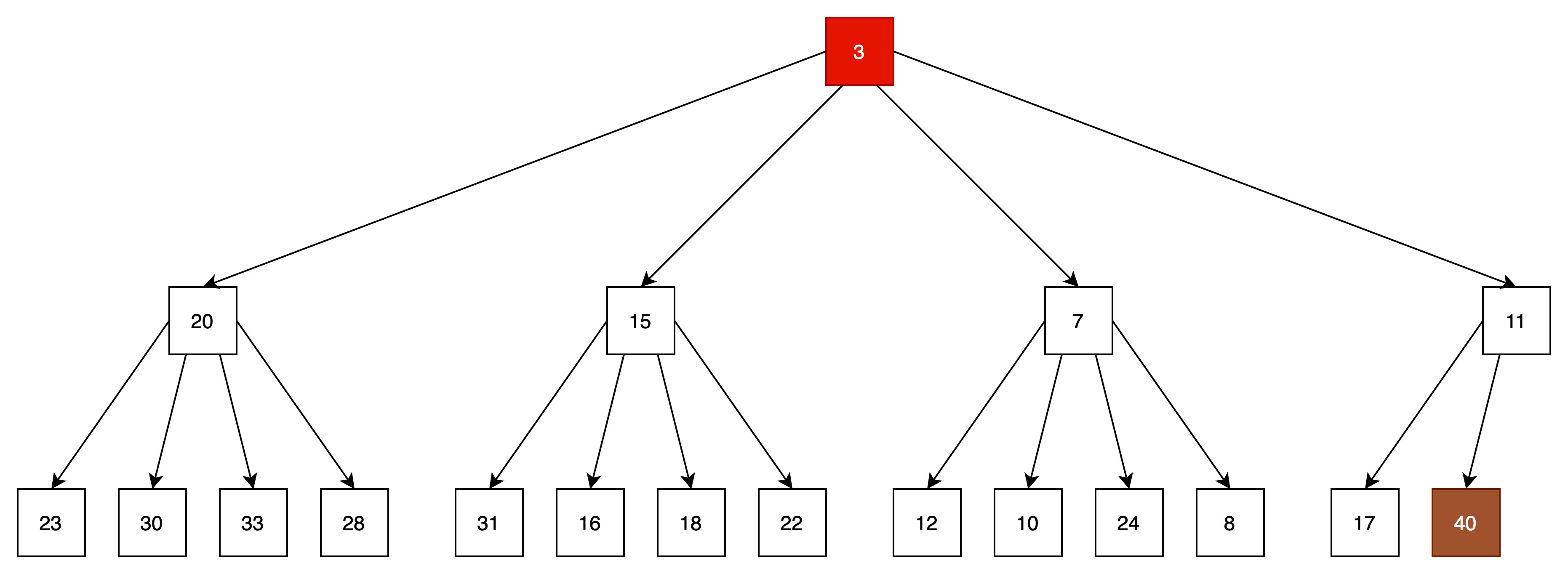
找到最后的元素40
(2)将最后的元素替换队头元素
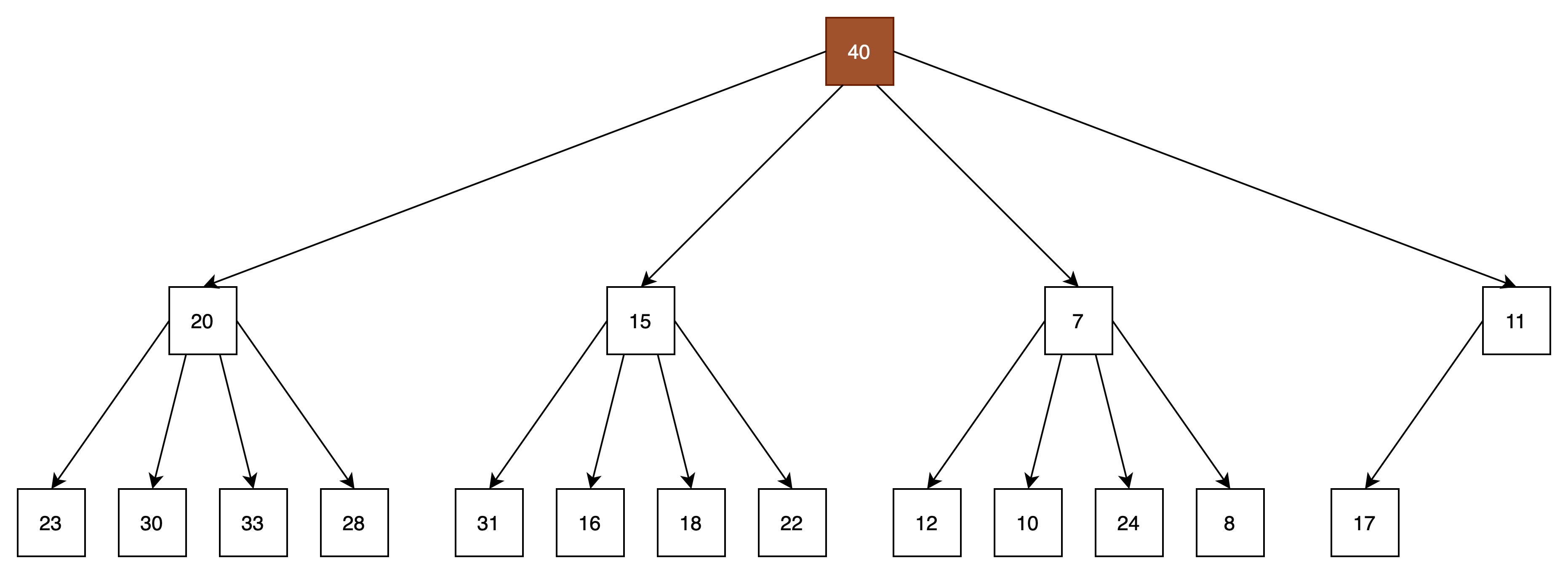
(3)向下过滤,找到当前结点的所有子结点中的最小结点,并与之进行比较,如果不满足堆的顺序性,则将此两个结点进行位置转移。
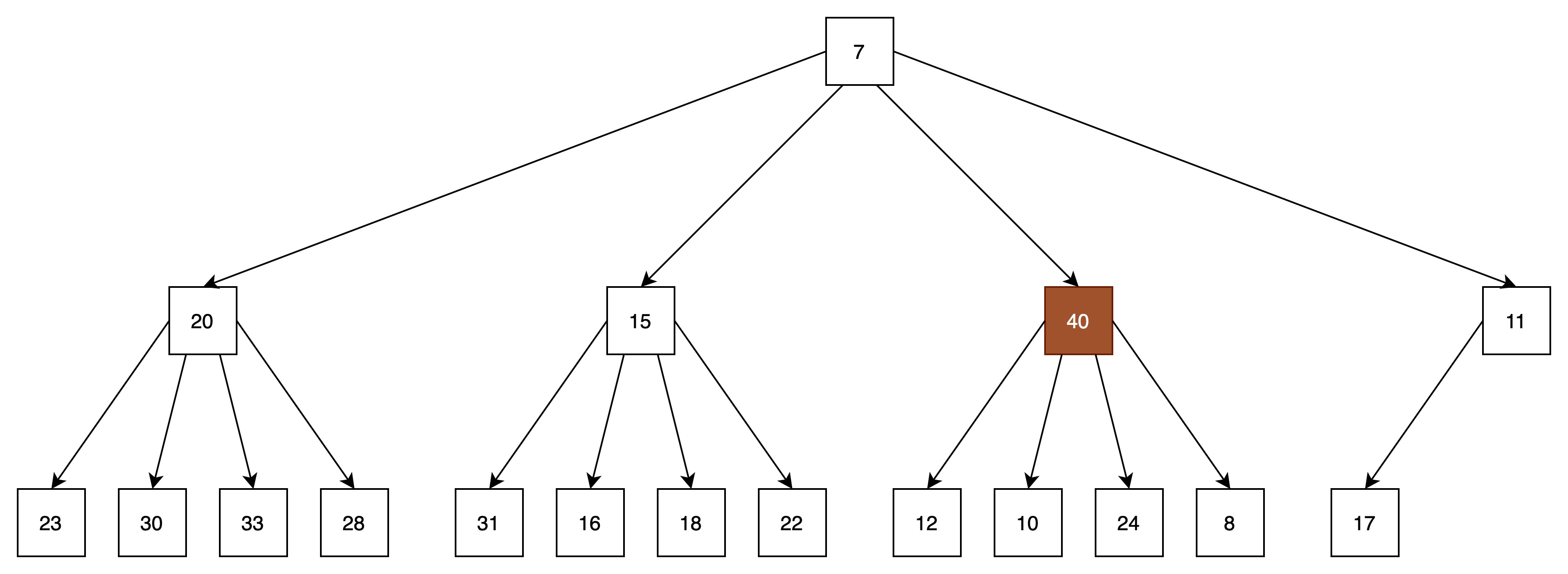
结点40和结点7进行位置转移。
(4)向下过滤,找到当前结点的所有子结点中的最小结点,并与之进行比较,如果不满足堆的顺序性,则将此两个结点进行位置转移。
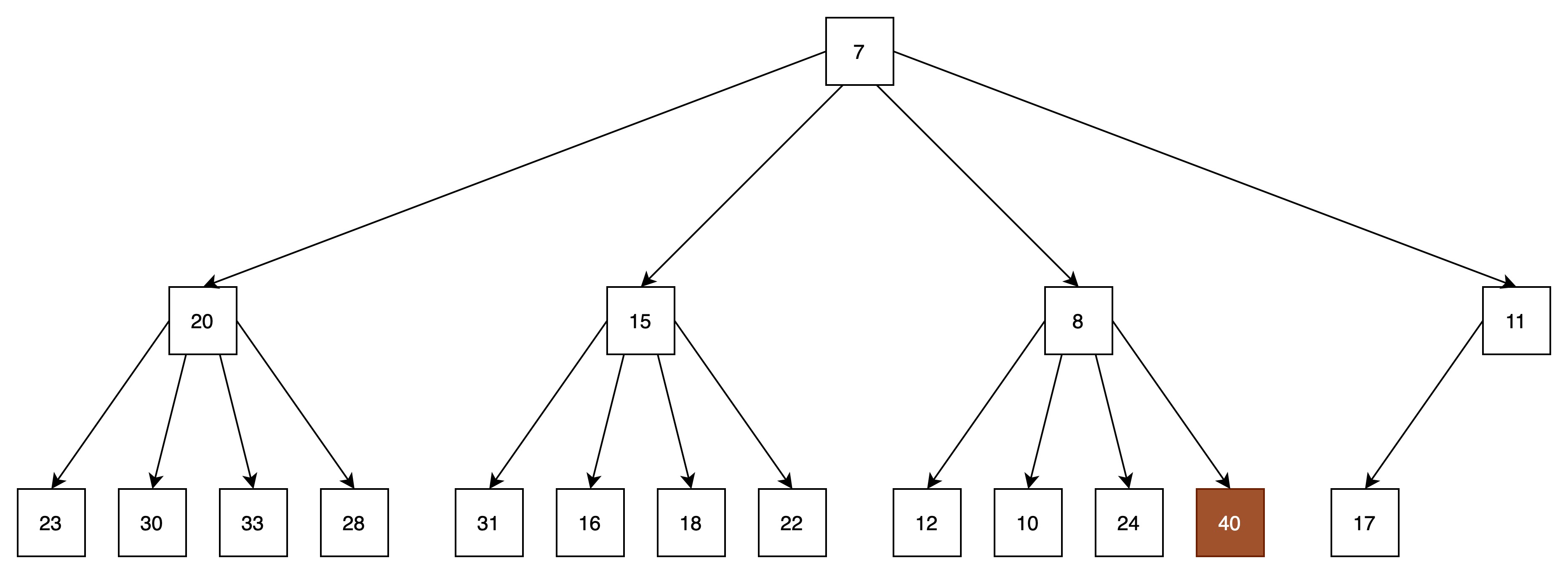
结点40与结点8进行位置转移。
当前结点与所有子结点关系满足堆的顺序性,或者当前结点为叶子结点,则向下过滤结束,完成出队操作。
3.D堆的适用场景
因为D堆的enQueue操作比deQueue操作简单,所以D堆主要被用在插入操作比删除操作多得多的场景中。或者当前优先级队列太大了,以至于不能完全放入内存,需要放在外存中,D堆很有用,它可以减少内存和外存的交换。