1.哈夫曼树概述

哈夫曼树是通过自底向上的方法构建的二叉树

1.1.哈夫曼树定义

给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

在计算机数据处理中，哈夫曼编码使用变长编码表对源符号（如文件中的一个字母）进行编码，其中变长编码表是通过一种评估来源符号出现机率的方法得到的，出现机率高的字母使用较短的编码，反之出现机率低的则使用较长的编码，这便使编码之后的字符串的平均长度、期望值降低，从而达到无损压缩数据的目的。

哈夫曼算法构造最优二叉树的算法过程如下：

（1）给定一个具有n个权值的结点集合{W1, W2, ……, Wn}，构造一片森林F={T1, T2, ……, Tn}，森林中每棵树都是只有根结点的二叉树，Ti树对应的权值为Wi

（2）初始时，设森林A=F

（3）执行n-1次循环，每个循环执行以下操作（1<=i<=n-1）

从当前森林中取最小和次小的两颗树，以这两颗树作为左右子树构建一颗新树Bi，Bi对应的权值为左右子树权值之和。从森林A种移除最小和次小的两个数，然后把Bi加入到A中。这样，在森林A种便少了一棵树。

经过n-1次循环后，森林A中只剩下一棵树，这棵树就是哈夫曼树。

这里从一段文本压缩，文本中每个字符出现的次数为权值，对这段文本进行编码。

（1）选取一段文本，字符出现频率统计如下

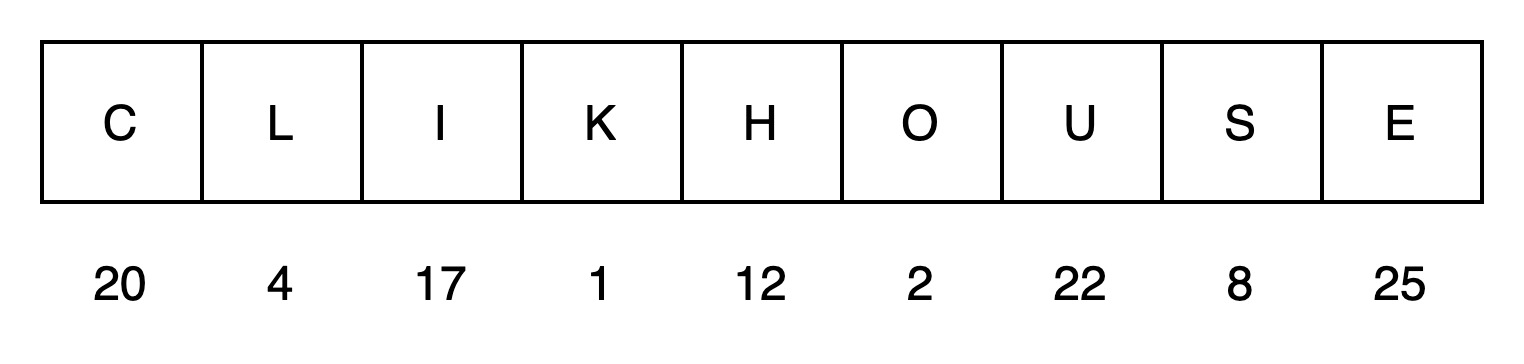
有9颗子树，需要进行8次循环

（2）第一次循环处理，归并K和O

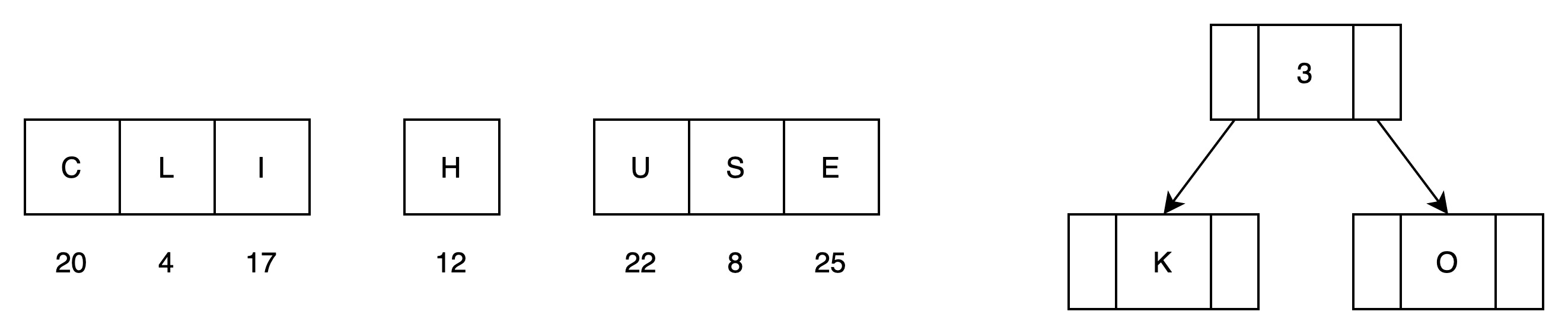
有8颗子树

（3）第二次循环处理，归并L

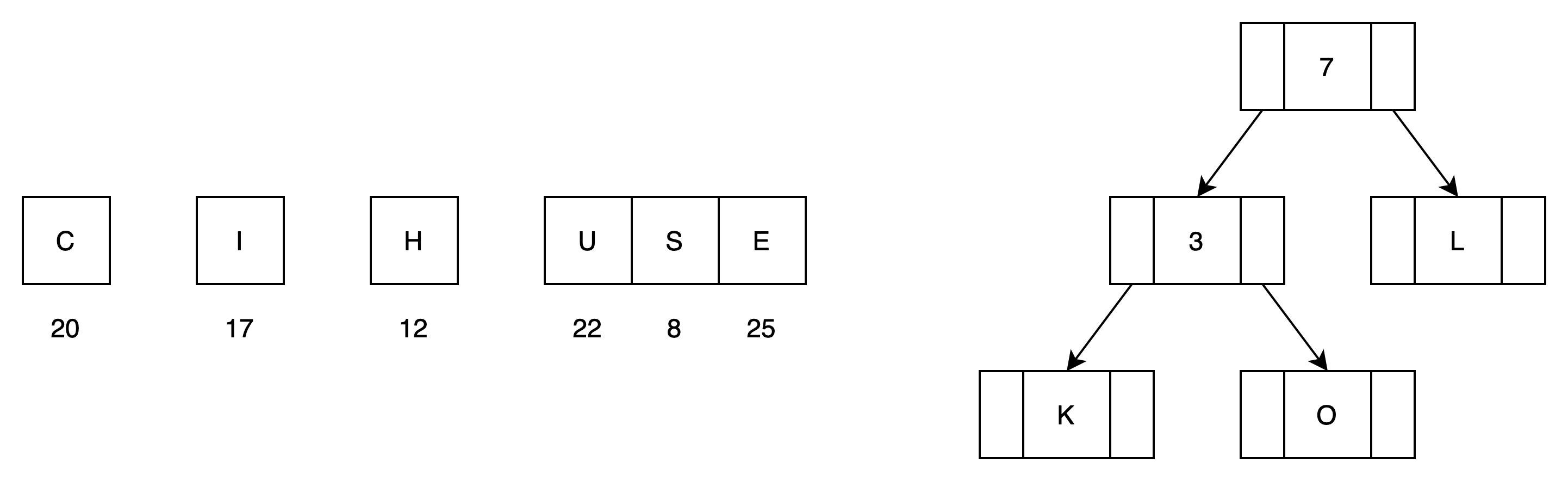
有7颗子树

（4）第三次循环处理，归并S

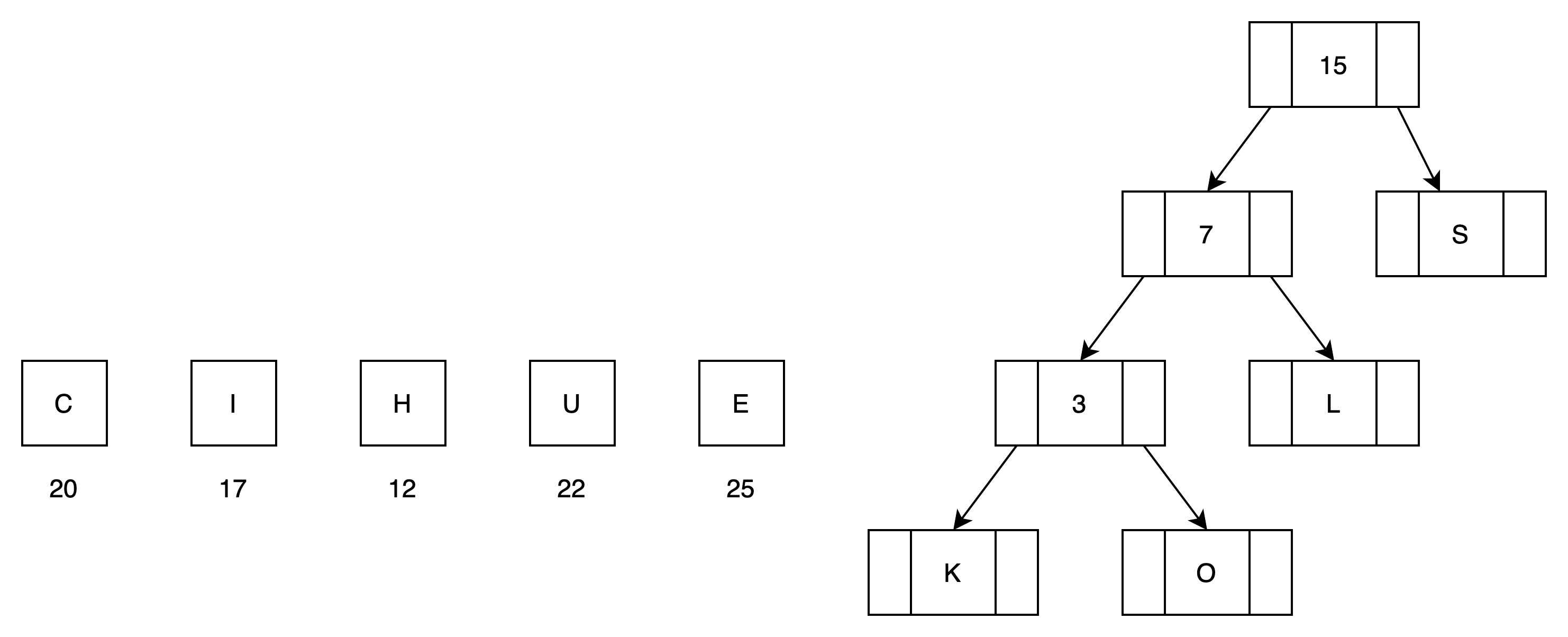
有6颗子树

（5）第四次循环处理，归并H

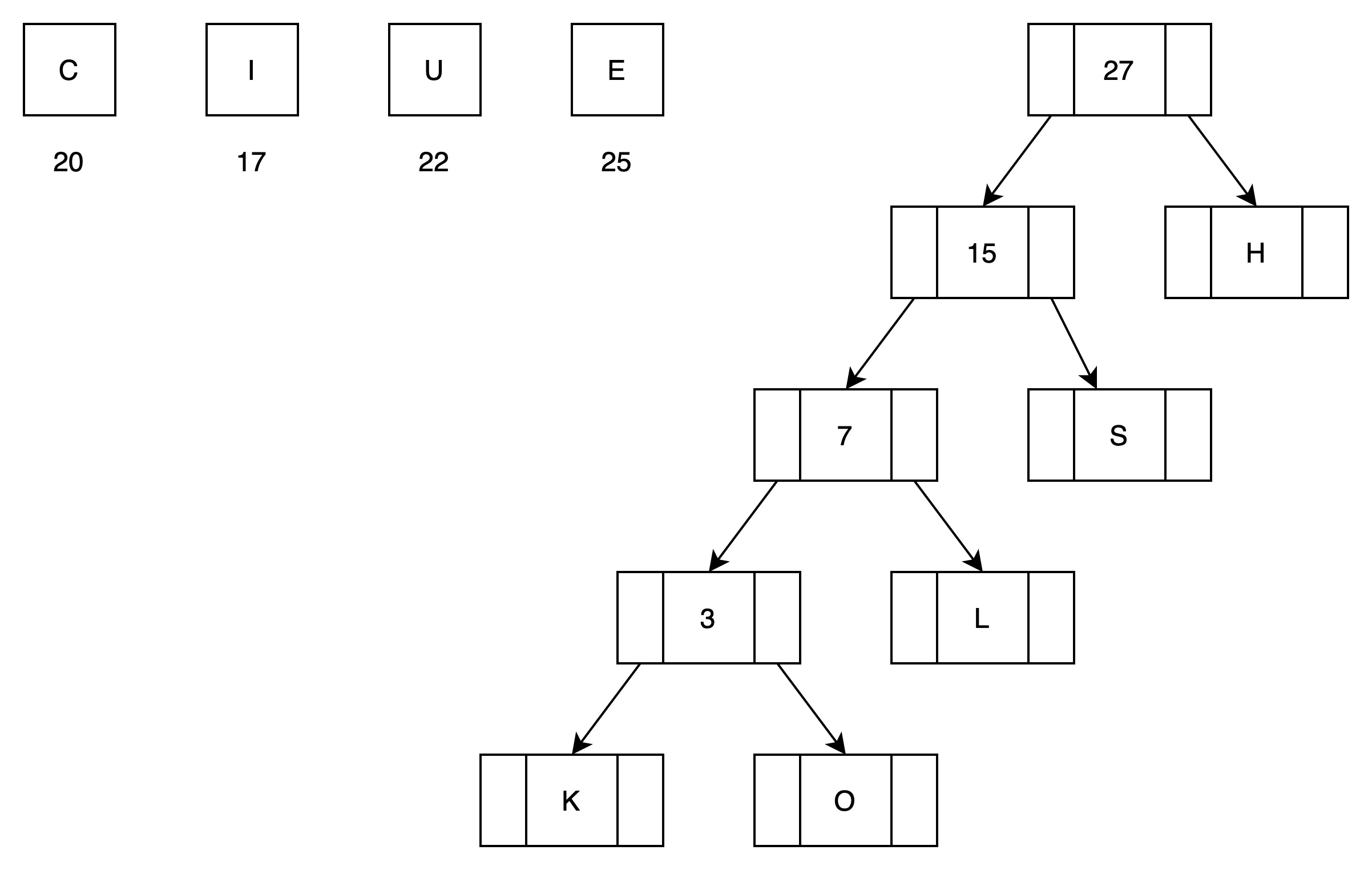
有5颗子树

（6）第五次循环处理，归并I和C

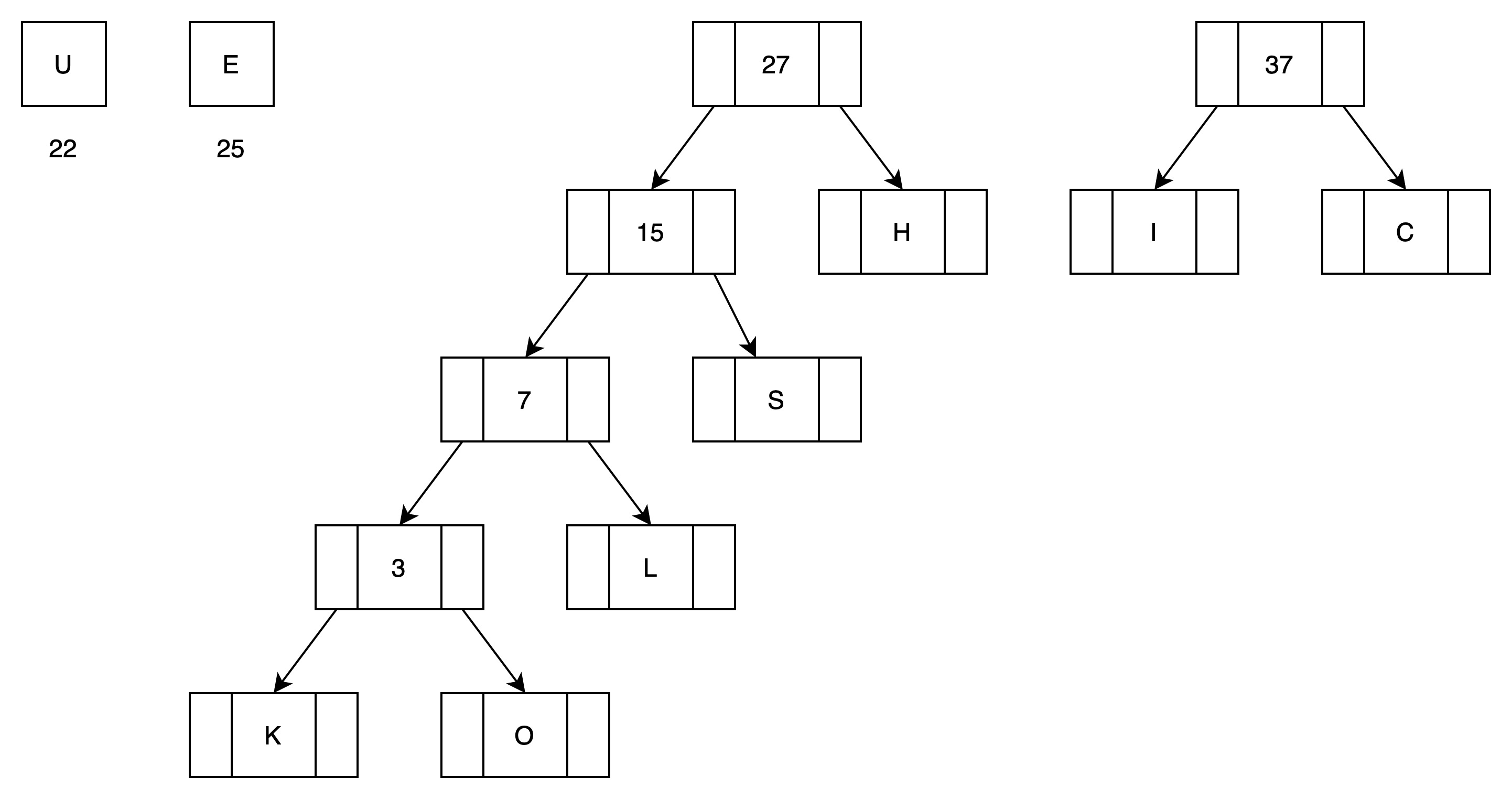
有4颗子树

（7）第六次循环处理，归并U

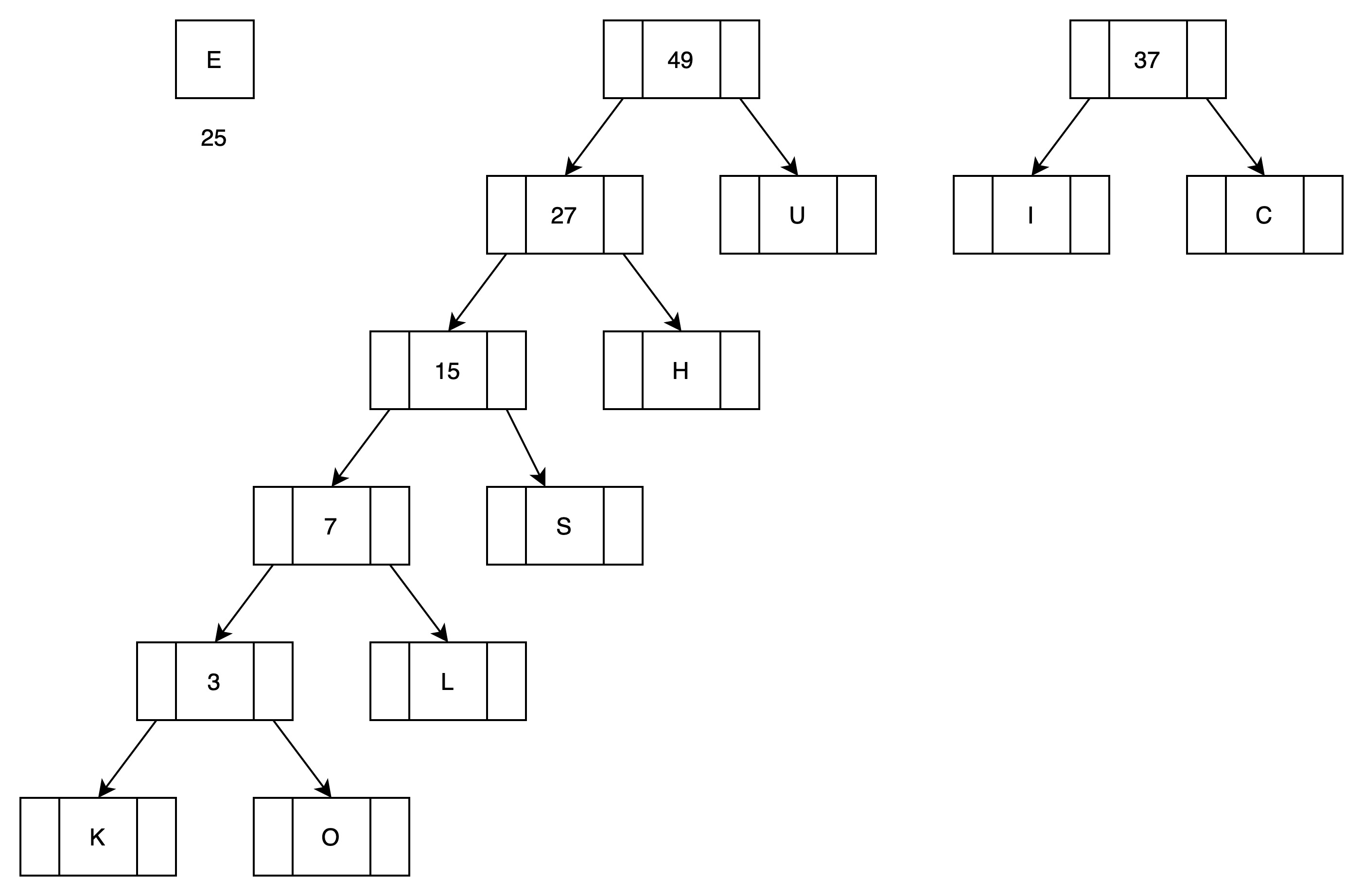
有3颗子树

（8）第七次循环处理，归并E

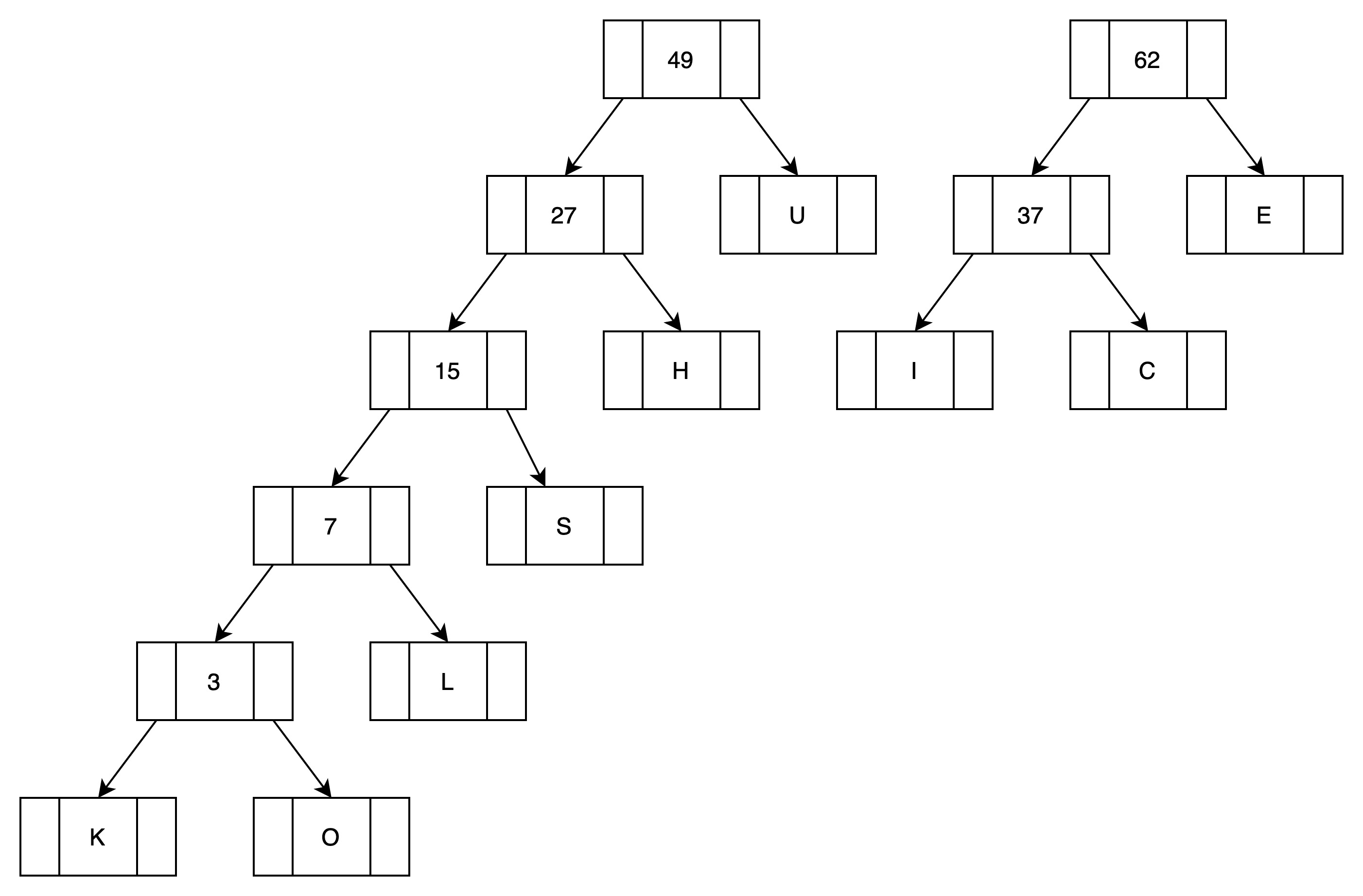
有两颗子树

（9）第八次循环处理，归并最后两颗子树

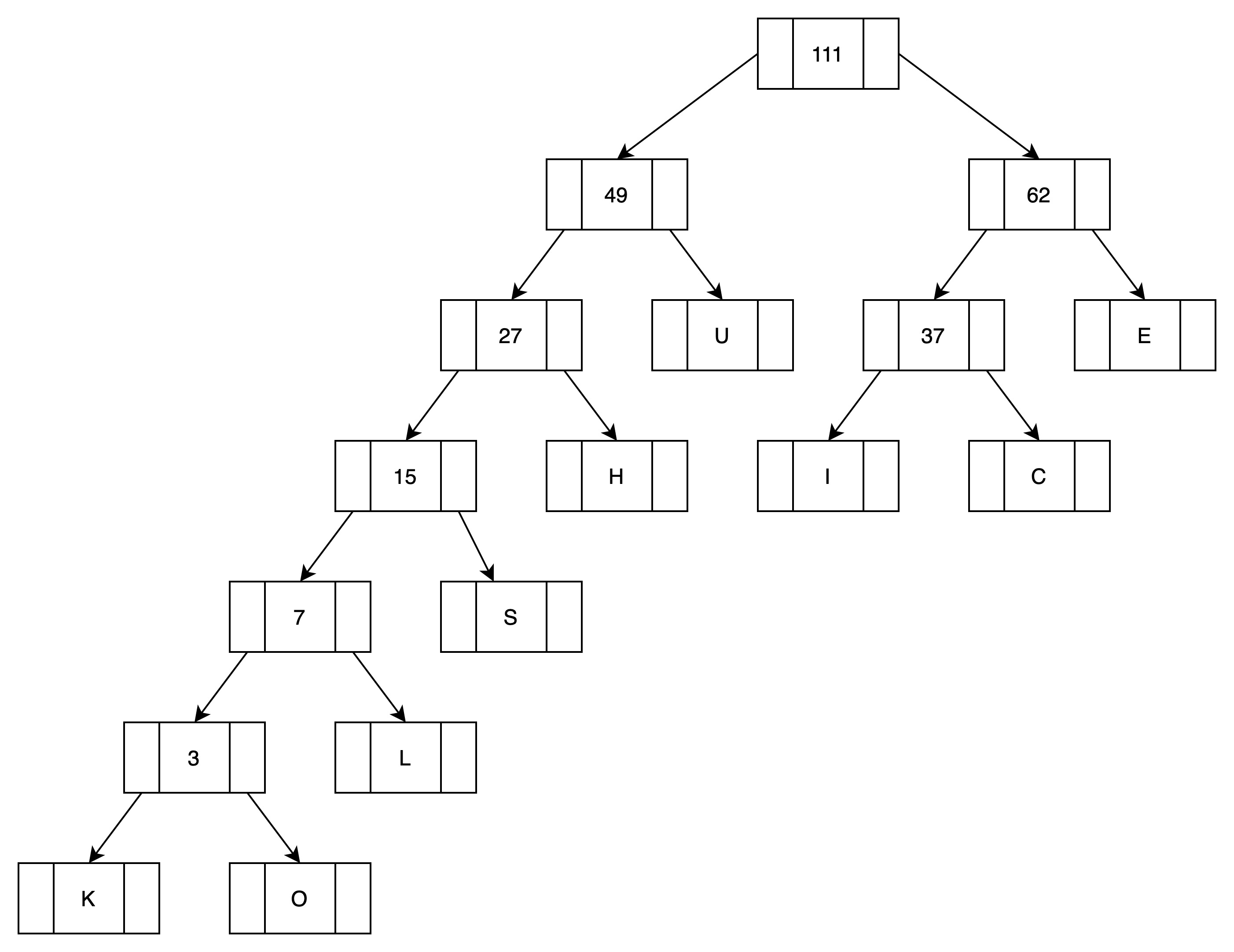
得到最终的一棵树，即哈夫曼树

（10）根结点无编码，其余左儿子结点编码为0，右儿子结点编码为1，根据以上哈夫曼树，得到所有叶子结点的编码，如下图所示：

这里可以看出，如果要保存这段文本，哈夫曼编码需要的存储量为6*1 + 6*2 + 5*4 + 4*8 + 3*12 + 2*22 + 3*17 + 3*20 + 2*25 = 311 bits

如果是等长编码，9个字符，每个字符编码为4位（2^3<9<=2^4），那么存储量为4*(1 + 2 + 4 +8 + 12 + 22 + 17 + 20 + 25) = 444 bits

可以看到，哈夫曼编码明显有压缩的作用。

从哈夫曼树来看，所有编码的结点都在叶子结点上，每个叶子结点往根结点溯源，都不会出现其他的叶子结点，也就是任何叶子结点的编码都不会包含其他结点，每个比特编码都能无二异性地解码。