1.二叉查找树概述

动态查找表既支持查找操作，又支持增、删、改操作。

用于处理动态查找表的树称为查找树。

1.1.二叉查找树的定义

二叉查找树是查找树的一种。

二叉查找树也称为二叉排序树，它可以是一颗空树，或者满足以下条件的二叉树：

（1）对于树中任一结点，如果其左子树不为空，则左子树所有元素的键值都比当前结点的键值小。

（2）对于树中任一结点，如果其右子树不为空，则右子树所有元素的键值都比当前结点的键值大。

（3）对于树中任一结点，它的左右子树都是二叉查找树。

1.2.二叉查找树示例

下图是一颗简单的二叉查找树

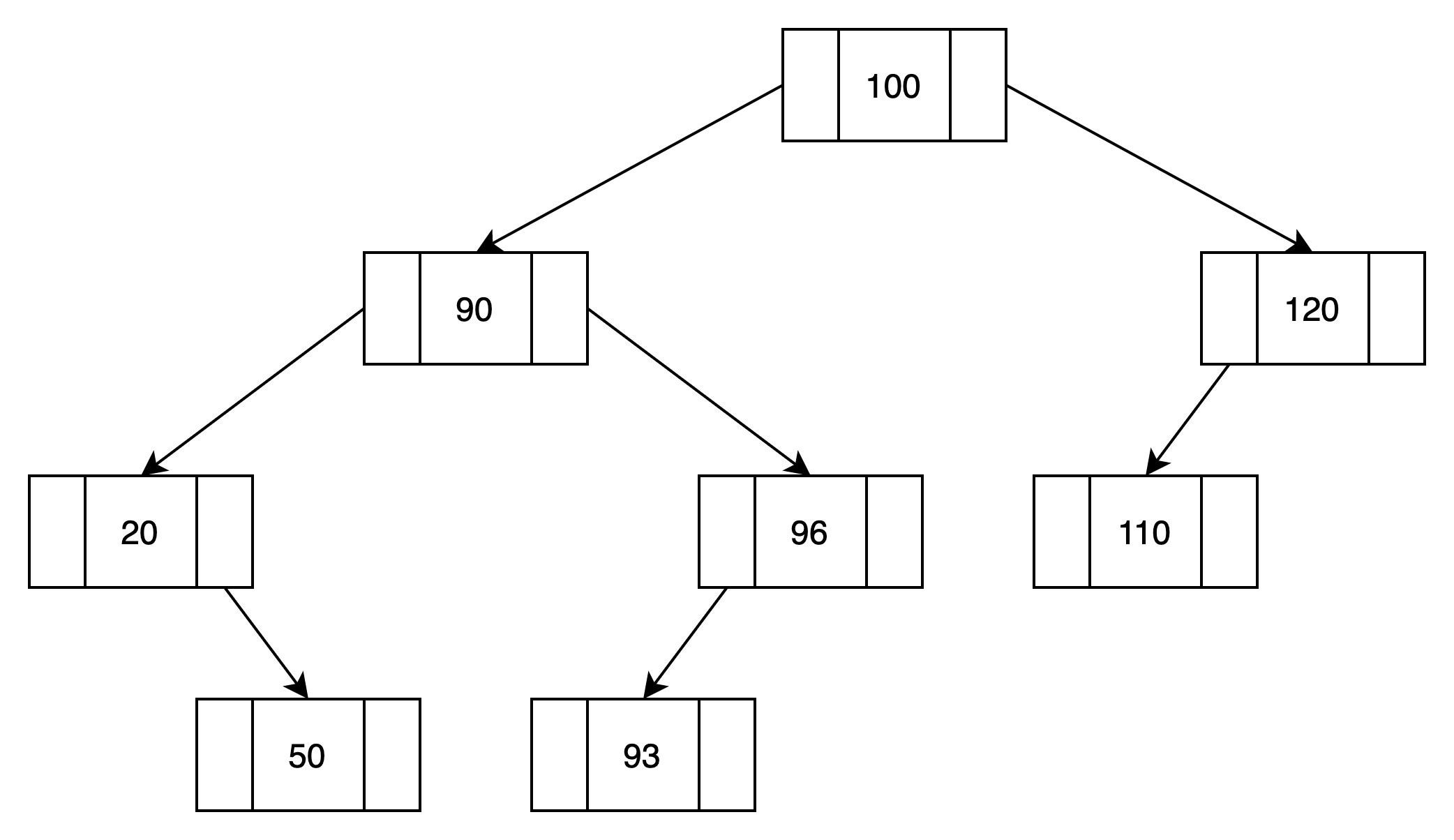
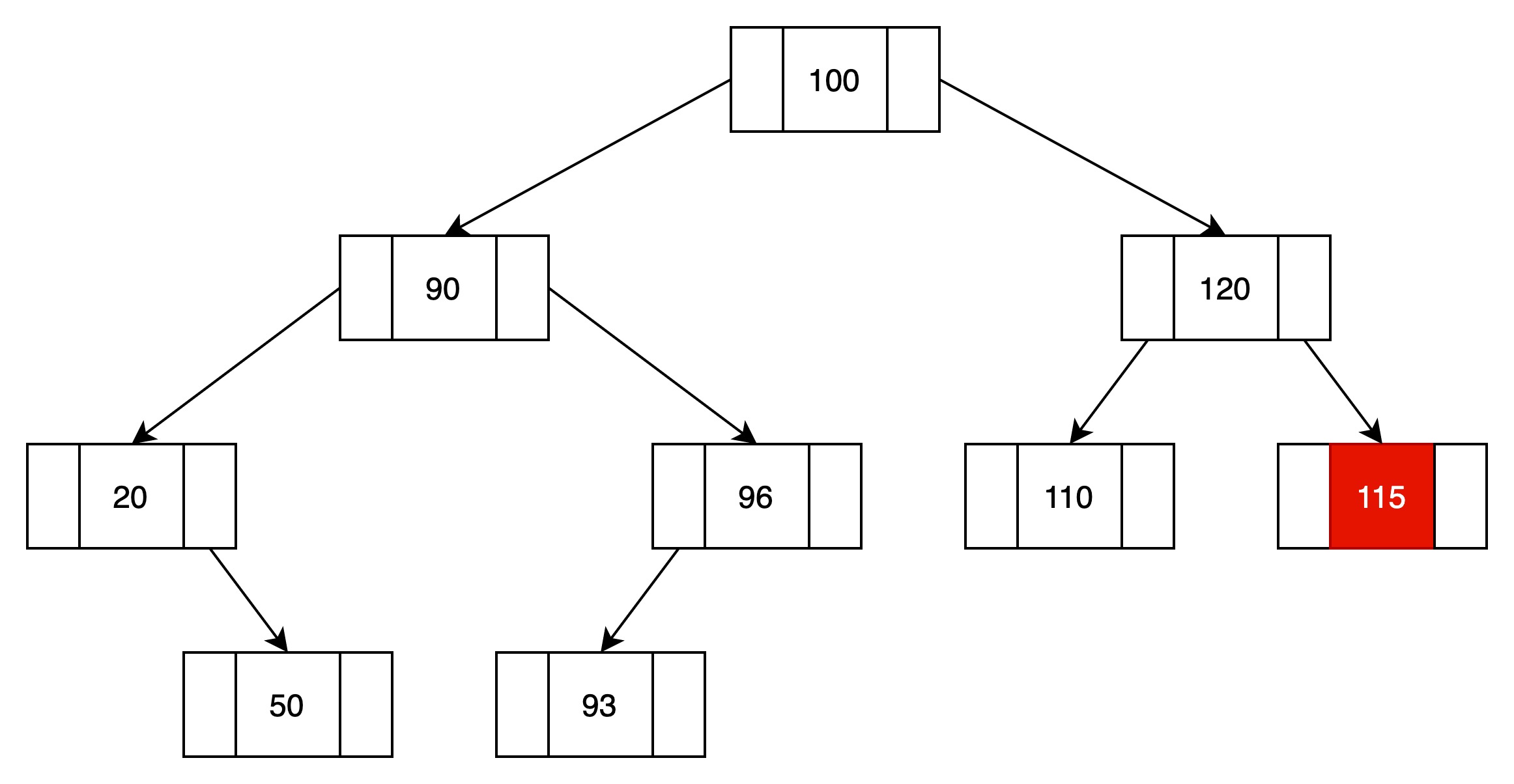
下图不是一颗二叉查找树，因为115结点违背了二叉查找树的条件。

2.二叉查找树的运算

二叉查找树支持以下三种基本操作：

2.1.find

查找特定元素在二叉查找树中是否存在。

2.1.1.find伪代码

如下所示：

boolean find(x, tree) { // 在tree中查找x元素
	if (树为空) return false;
	else if (根结点 == x) return true;
	else if (x < 根结点) return find(x, tree.left); // 左子树递归查找x
	else return find(x, tree.right); // 右子树递归查找
}

2.1.2.find案例

下面是一颗二叉查找树，如果要查找key为93的元素，查找过程如下：

（1）与根结点对比

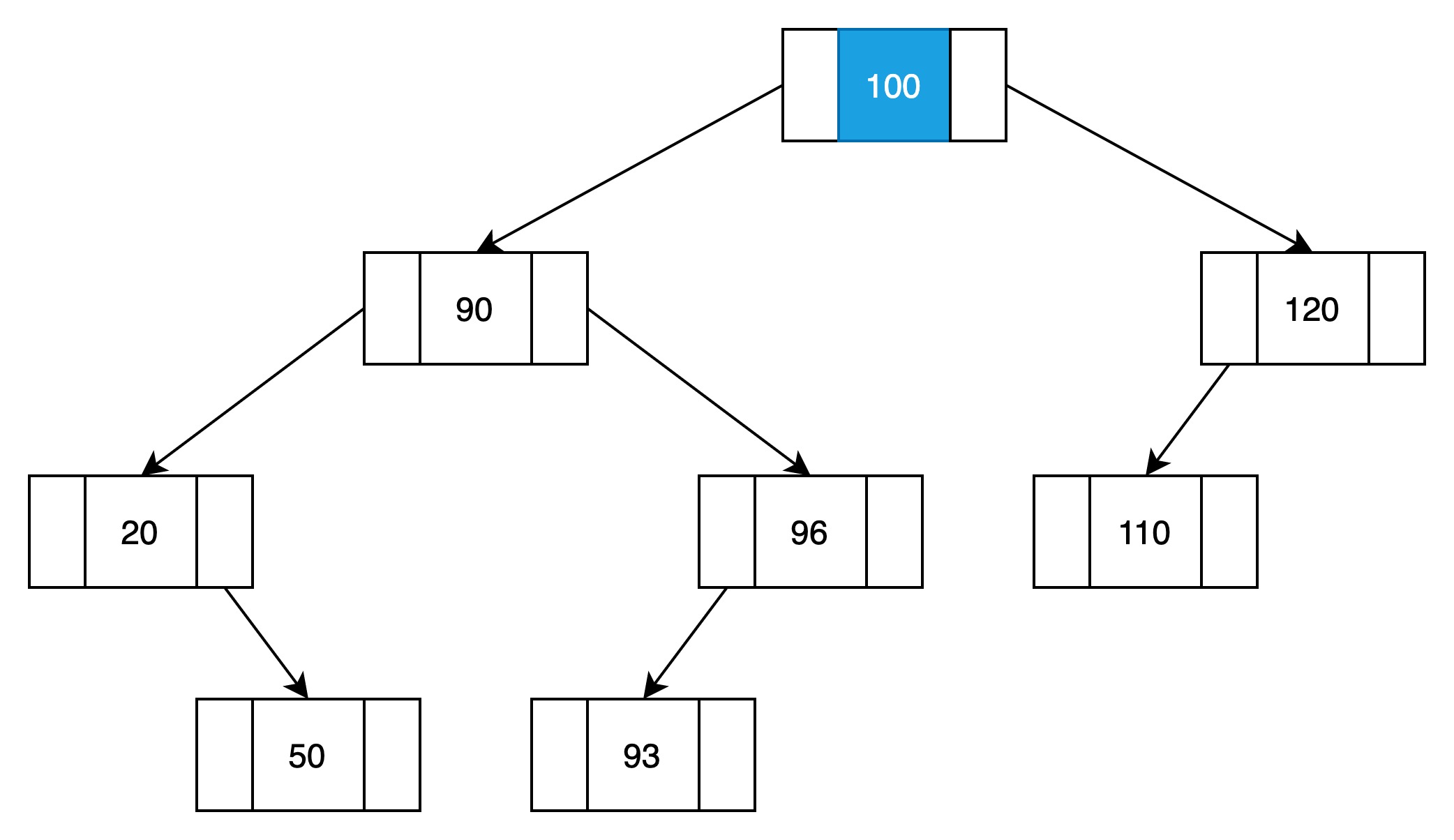
比100小，则向左子树查找

（2）与结点90对比

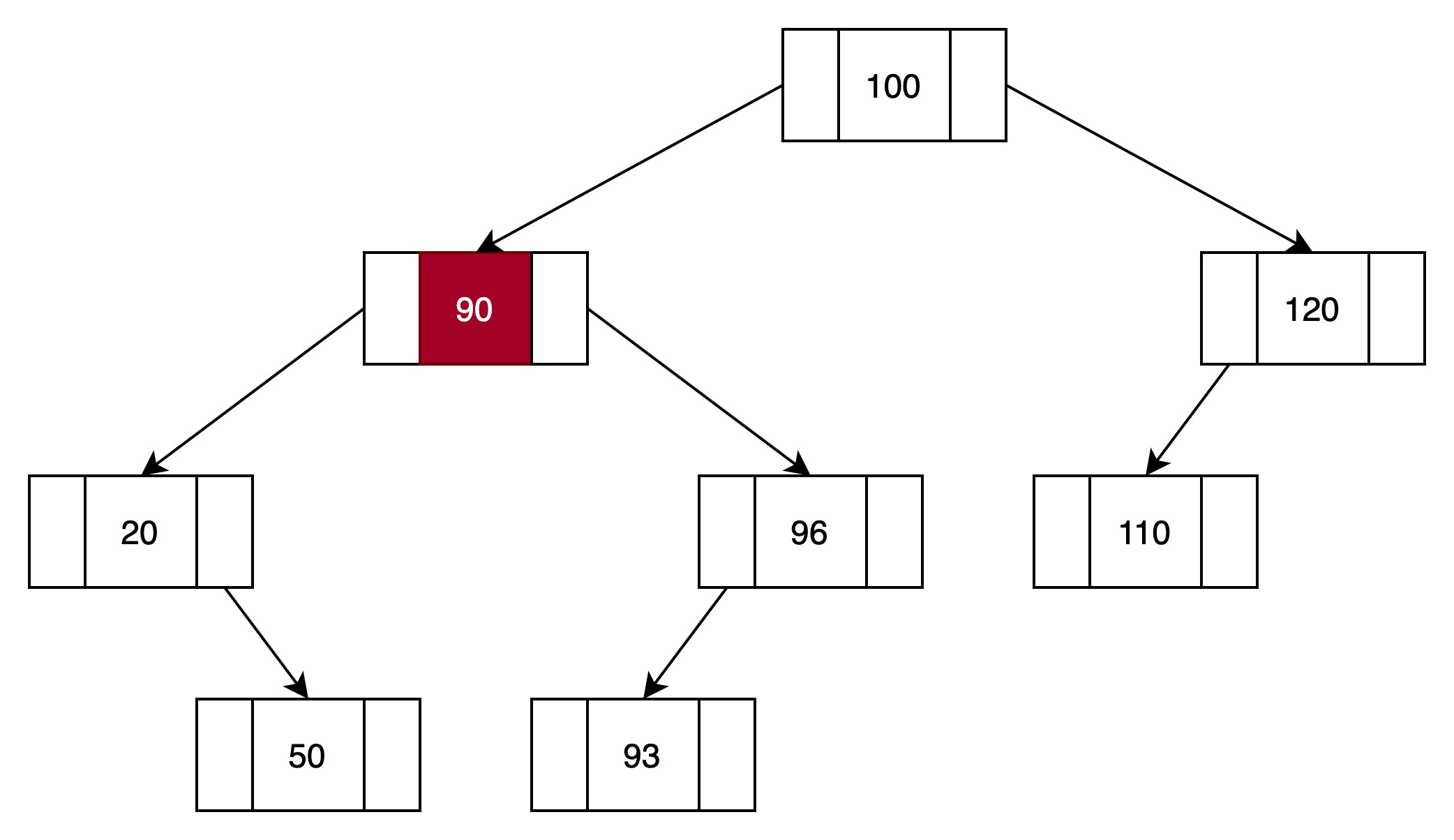
比90大，向右子树查找

（3）与结点96对比

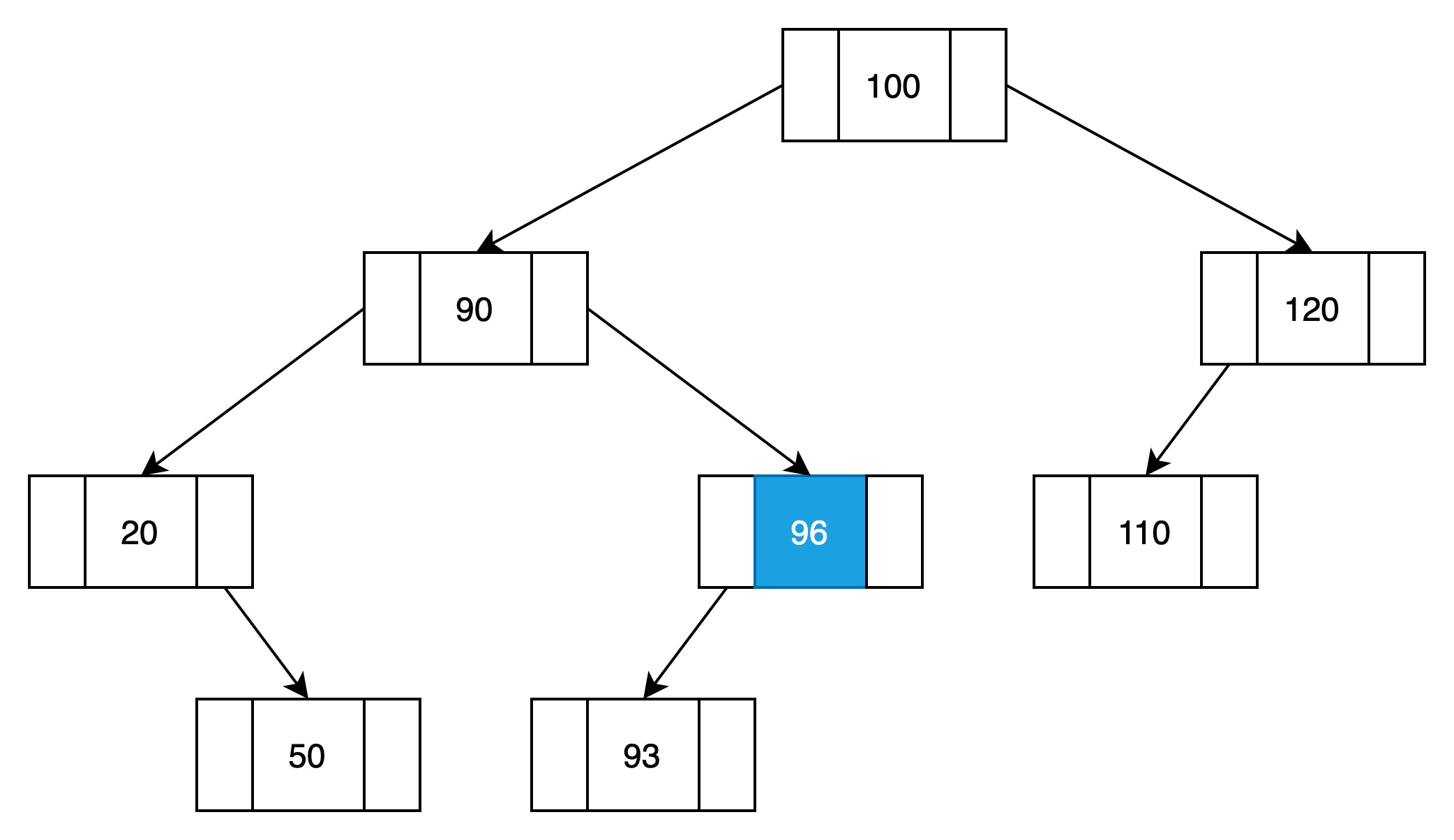
比96小，向左子树查找

（4）与结点93对比

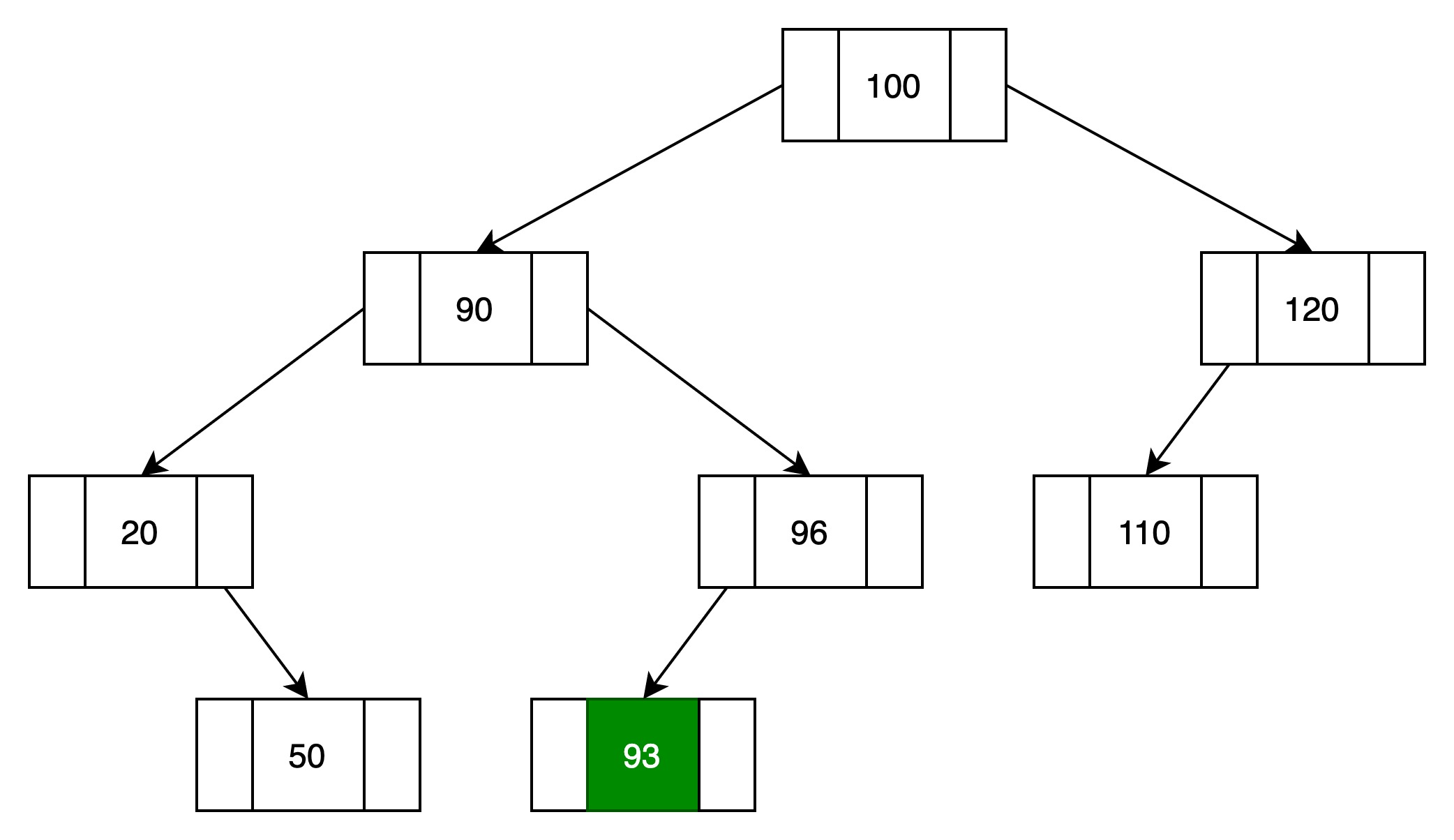
当前结点key值相等，返回当前结点

共经历了4次对比。

2.2.insert

在二叉查找树中插入一个新元素

2.2.1.insert伪代码

如下所示

void insert(x, tree) {
	if (树为空) {
		申请一个结点存放x
		将结点设为根结点
	} else {
		if (根结点 == x) {
			结点已存在，直接返回
		} else if (x < 根结点) {
			insert(x, tree.left) // 在左子树插入
		} else {
			insert(x, tree.right) // 在右子树插入
		}
	}
}

2.2.2.insert案例

在如下二叉查找树中插入一个新元素115，过程如下

（1）与结点100对比

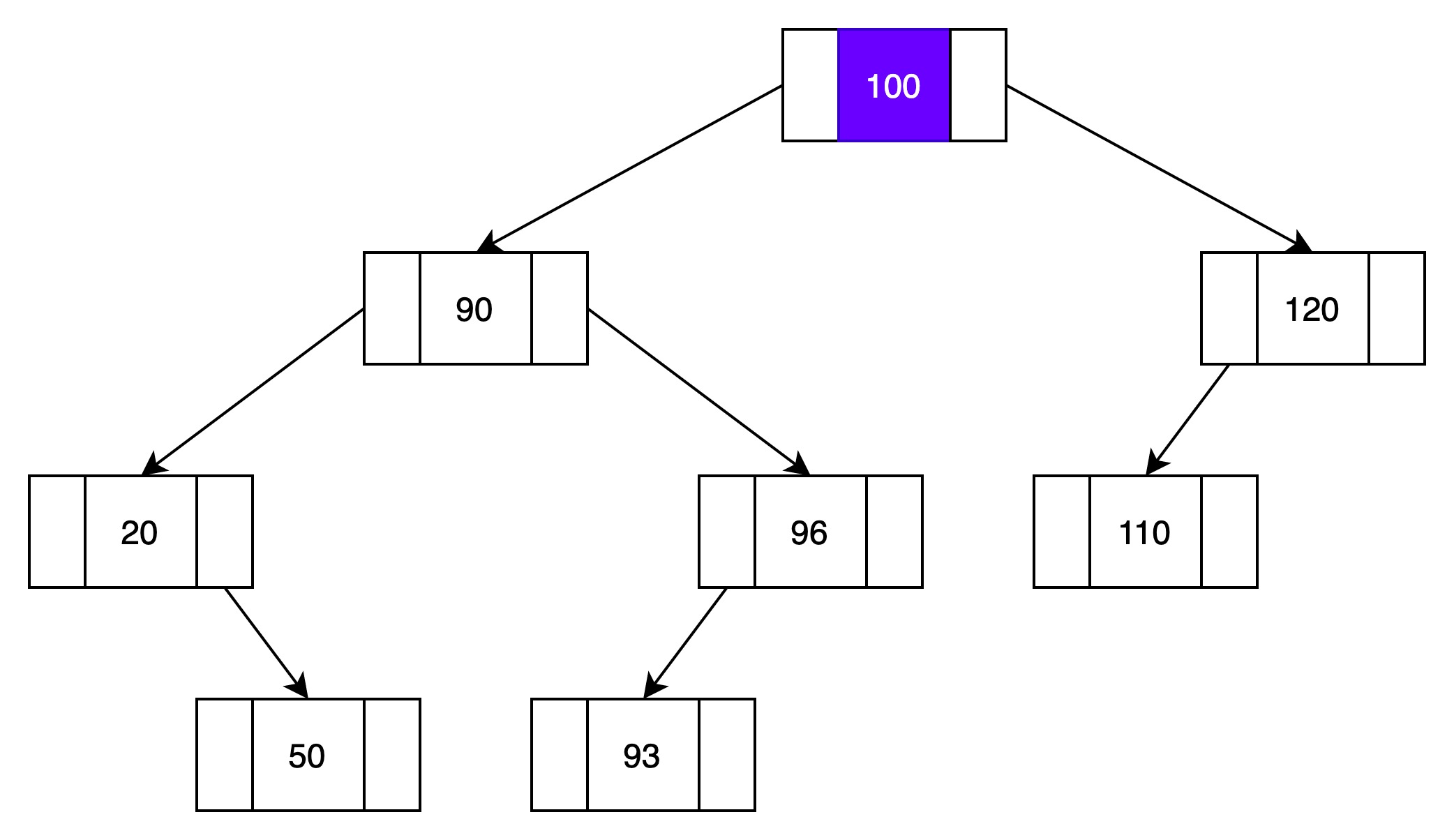
115比100大，插入右子树

（2）与结点120对比

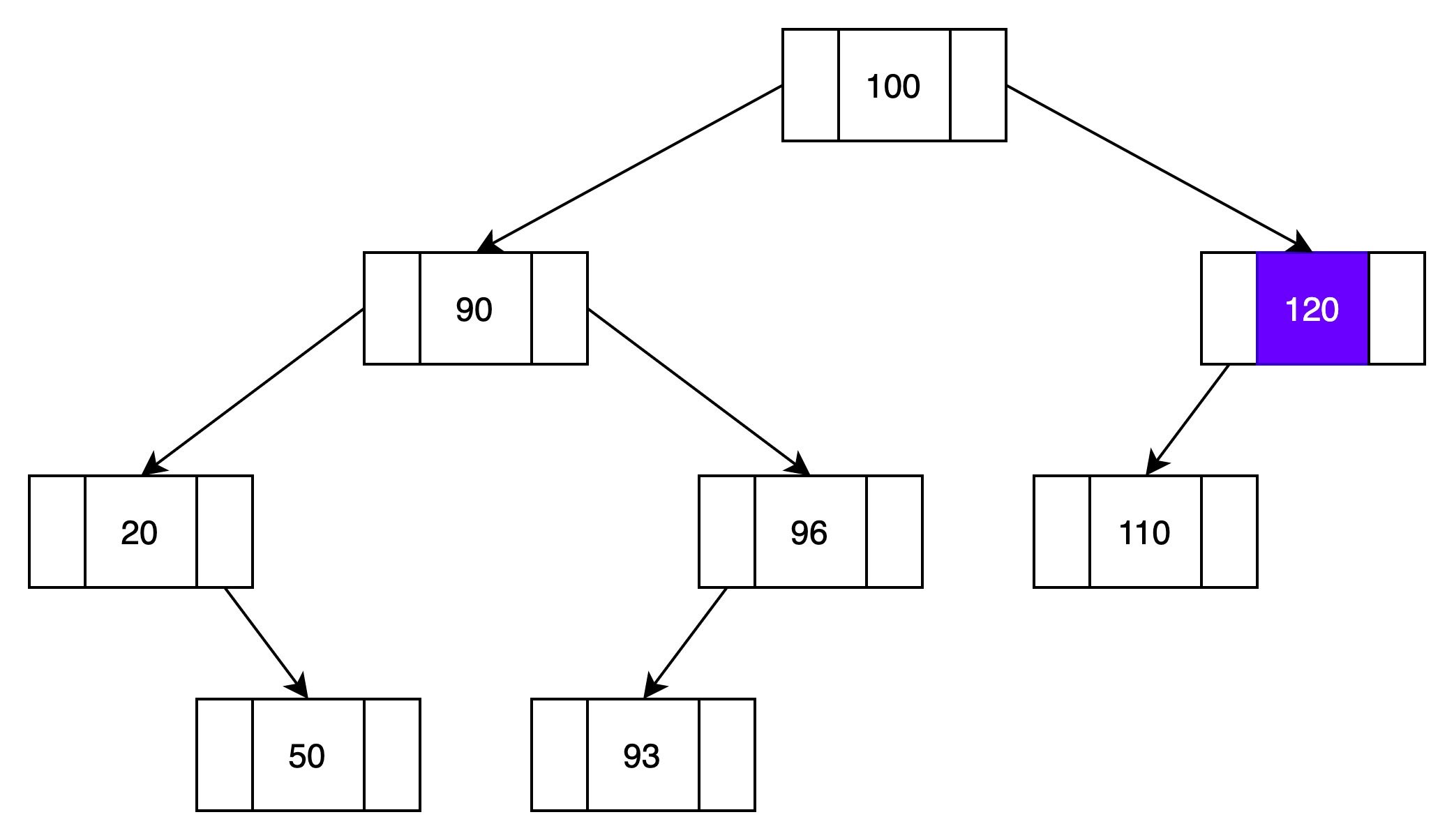
115比120小，插入左子树

（3）与结点110对比

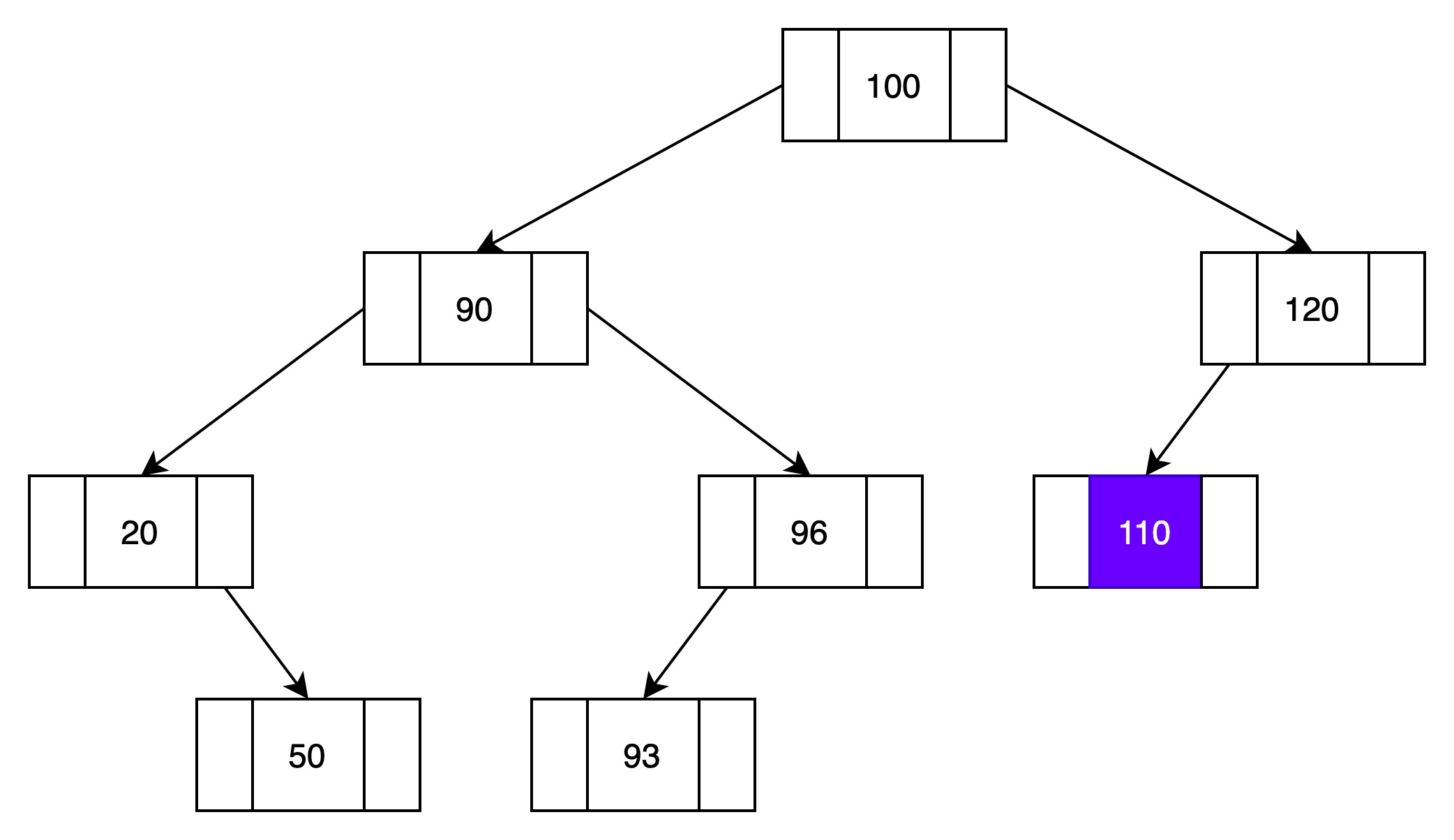
115比110大，插入右子树

（4）110的右子树为空，则新增元素作为110的右子树

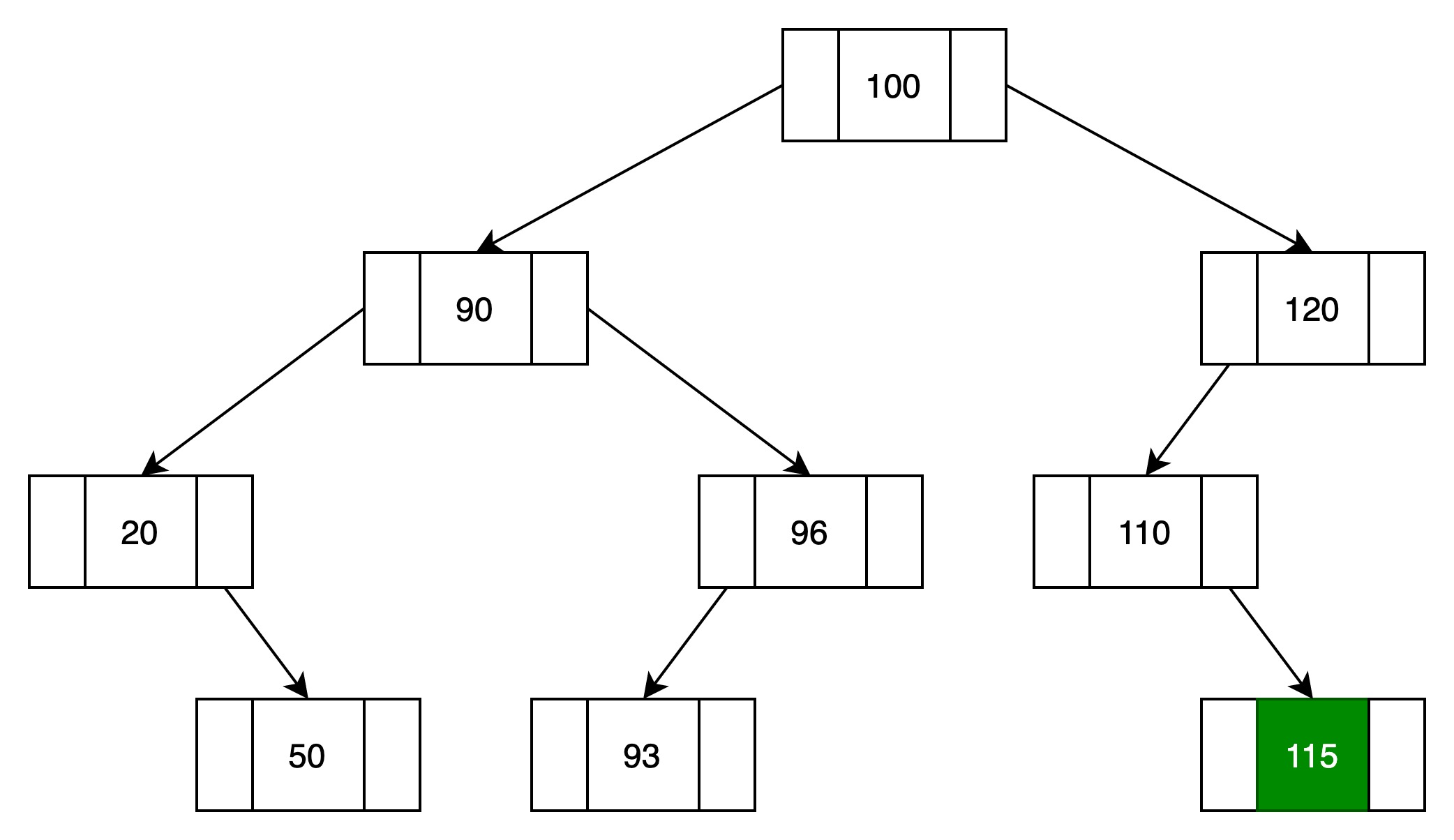
插入结束，得到一颗新的二叉查找树。

2.3.remove

在二叉查找树中删除一个元素。

2.3.1.remove伪代码

如下所示：

void remove(x, treeNode) {
	if (treeNode为空) {
		直接返回
	} else {
		if (x > treeNode.value) {
			remove(x, treeNode.right) // 在右子树上删除结点
		} else if (x < treeNode.value) {
			remove(x, treeNode.left) // 在左子树上删除结点
		} else { // x等于根结点值，删除当前结点
			if (treeNode.right不为空且treeNode.left不为空) { // 根结点有左右子树
				将treeNode.right中的最小值放入根结点
				在treeNode.right中删除最小值结点
			} else if (treeNode.right为空且treeNode.left不为空) { // 根结点只有左子树
				左子树取代根结点，删除原来的根结点
			} else { // 根结点只有右子树
				右子树取代根结点，删除原来的根结点
			}
		}
	}
}

2.3.2.remove案例

下面是一颗二叉查找树，从树中删除结点90，过程如下：

（1）与结点100对比

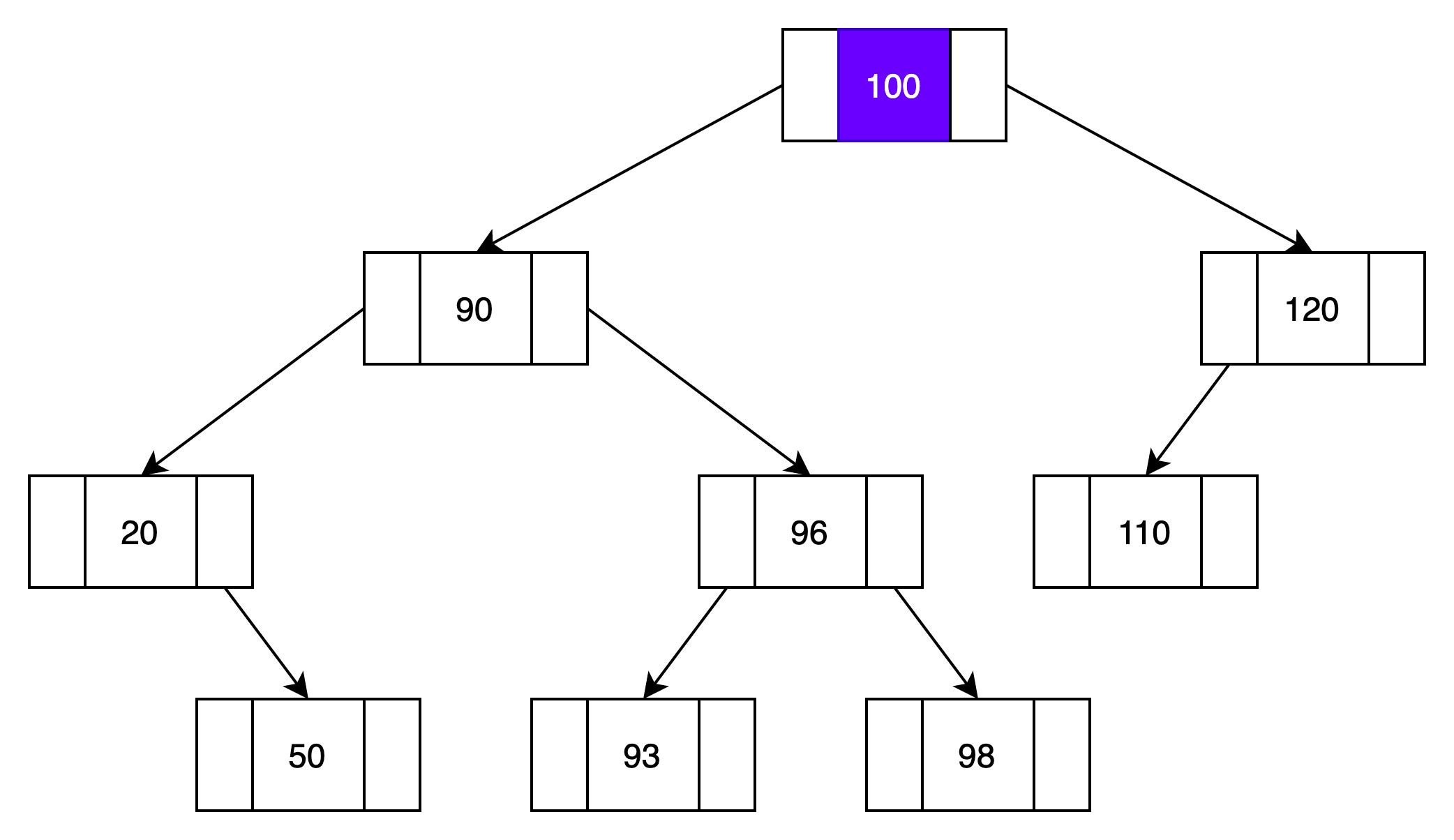
90比100小，从左子树删除

（2）与结点90对比

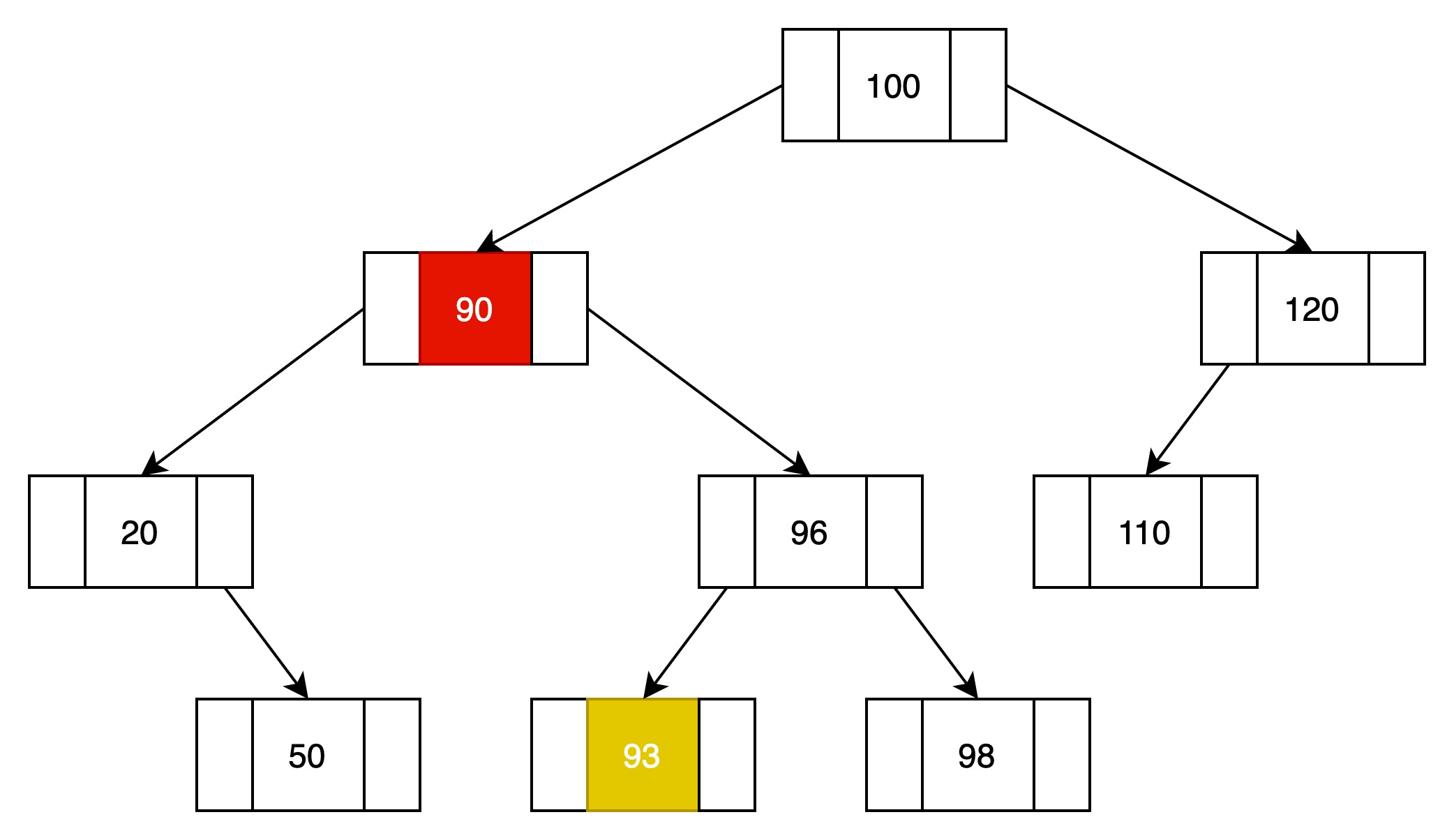
结点值匹配成功，则删除当前结点。同时找到当前结点右子树上的最小值93。

（3）结点93替换掉结点90

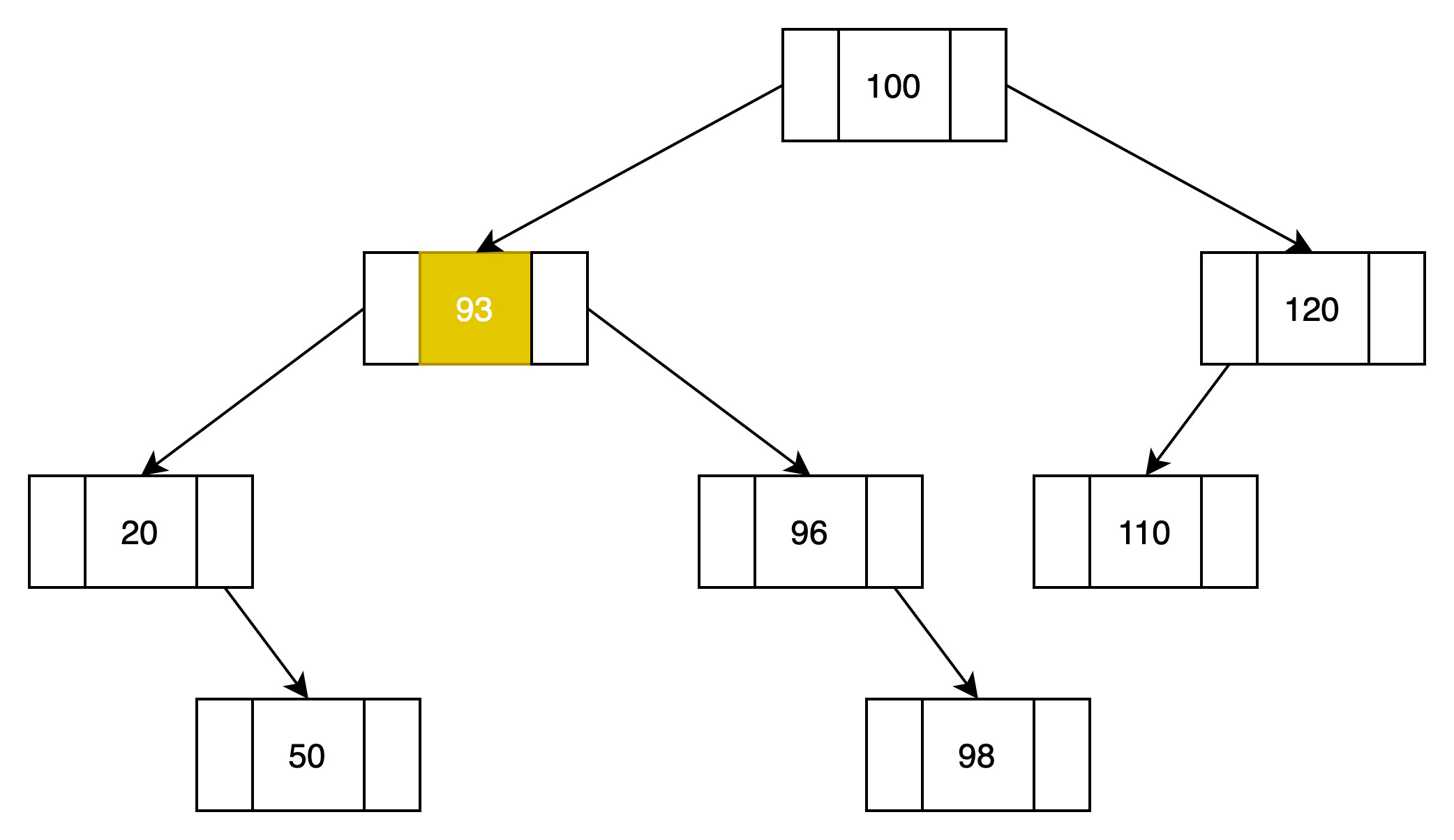
至此，remove成功。

找一棵树的最小值非常简单：沿着这棵树的左儿子递归查找，直到找到某个结点的左儿子为空，则此结点为最小结点。

同理，找一棵树的最大值也非常简单：沿着这棵树的右儿子递归查找，直到找到某个结点的右儿子为空，则此结点为最大结点。

从二叉查找树的条件可以看出，二叉查找树是递归定义的，所以以上运算的实现也往往是递归实现的。

3.二叉查找树的性能

二叉查找树的操作代价与过程中要访问的结点树成正比。访问结点数越多，性能越差。

因为没有其他条件限制，最坏的情况下，二叉查找树会退化为一个单链表。此时，查找时间复杂度为O(N)

最好的情况下，二叉查找树是完全平衡的，查找的时间复杂度为O(longN)

实践发现，平均情况下，查找代价比最好的情况高出38%，即1.38logN，所以平均时间复杂度还是O(logN)