1.AVL树概述
二叉查找树退化为单链表后,其操作的时间复杂度为O(N),二叉查找树的优点无法发挥。为了解决这一困境,两个苏联数学家在1962年提出了平衡树的概念。
AVL树满足二叉查找树的有序性。
1.1.AVL树定义
AVL树,也称为二叉平衡查找树,是将满二叉树的平衡条件稍微放宽,要求左右子树的高度差控制在一定范围内。
AVL树中,每个结点的左右子树高度差只能为1、0、-1三种。
1.2.结点平衡度
AVL树用平衡因子来衡量结点的平衡度。
结点的平衡度是结点的左子树高度减去右子树高度。
空树的高度定义为-1,即空树的平衡度为-1
1.3.AVL树的高度
AVL树的平衡条件表明了树只有对数级别的高度。
一颗有N个结点的AVL树,它的高度H小于或等于1.44log(N+1)-0.328
1.4.AVL树案例
下面是一颗AVL树。
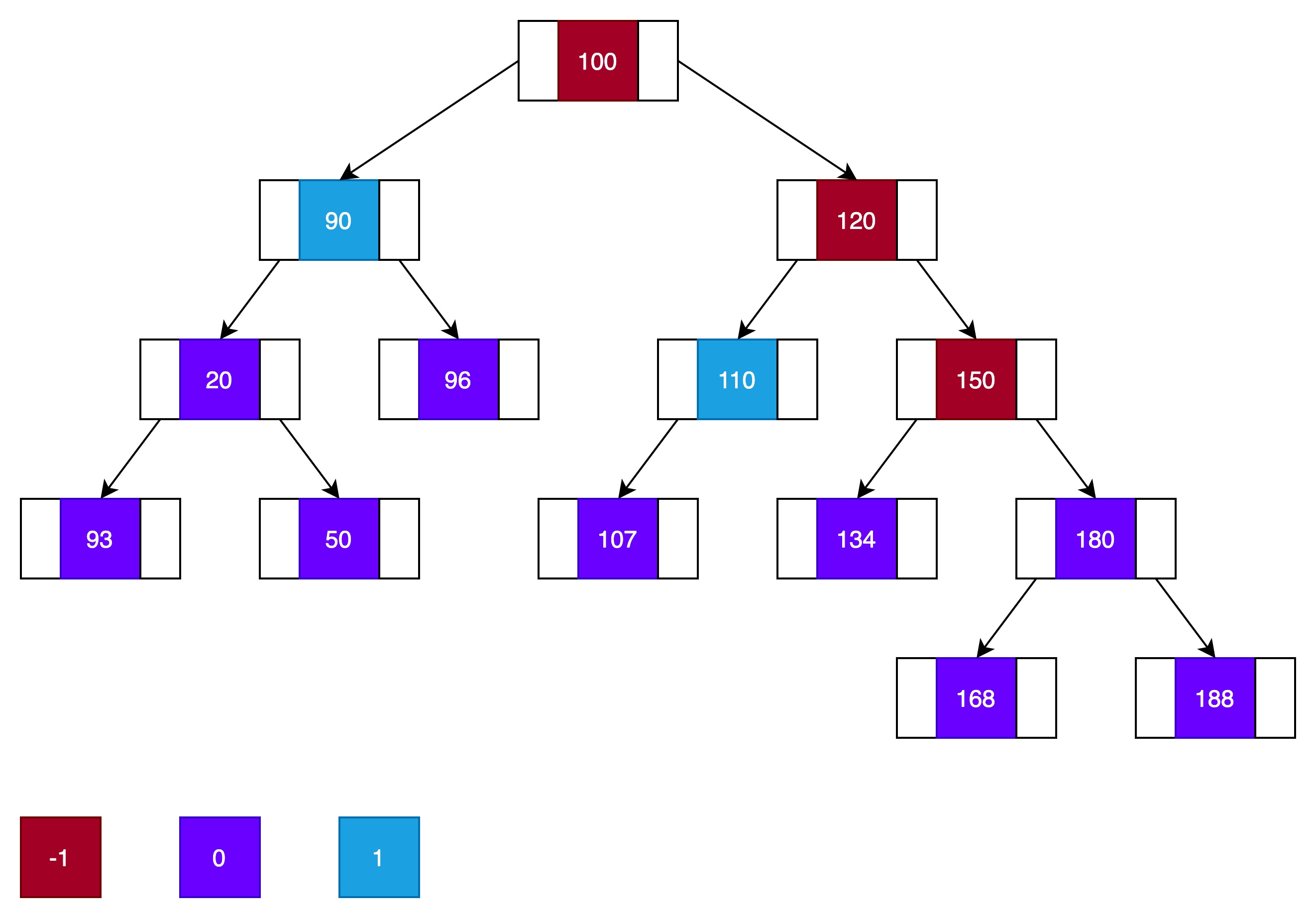
上图中,褐色表示平衡因子为-1,紫色表示平衡因子为0,蓝色表示平衡因子为1。
如果把结点134删除,则结点150的平衡度调整为-1,那么此树就不是一颗AVL树。
2.AVL树运算
AVL树有以下3种基本操作。
2.1.find
因为find操作不会影响树的平衡性,所以与二叉查找树的算法完全一致。
2.2.insert
AVL树的插入操作分为两步:第一步数据结点插入;第二步结点平衡。
在第一步数据结点插入过程中,操作算法与二叉查找树完全一致。
在第二步中,对于因新结点插入导致不平衡的结点,需要进行重新平衡操作。
在一次插入后,只有在插入点到根结点路径上的结点才有可能发生平衡因子的变化。如果在插入点往根结点回溯过程中,解决第一个出现不平衡的结点的平衡性问题,就能保证整颗树的平衡特性。
重新平衡有以下四种场景。
2.2.1.LL场景
原来A的左子树比右子树高,插入操作发生在A的左儿子的左子树中,使得A的左子树增高。
2.2.1.1.LL场景图示
如下图所示:
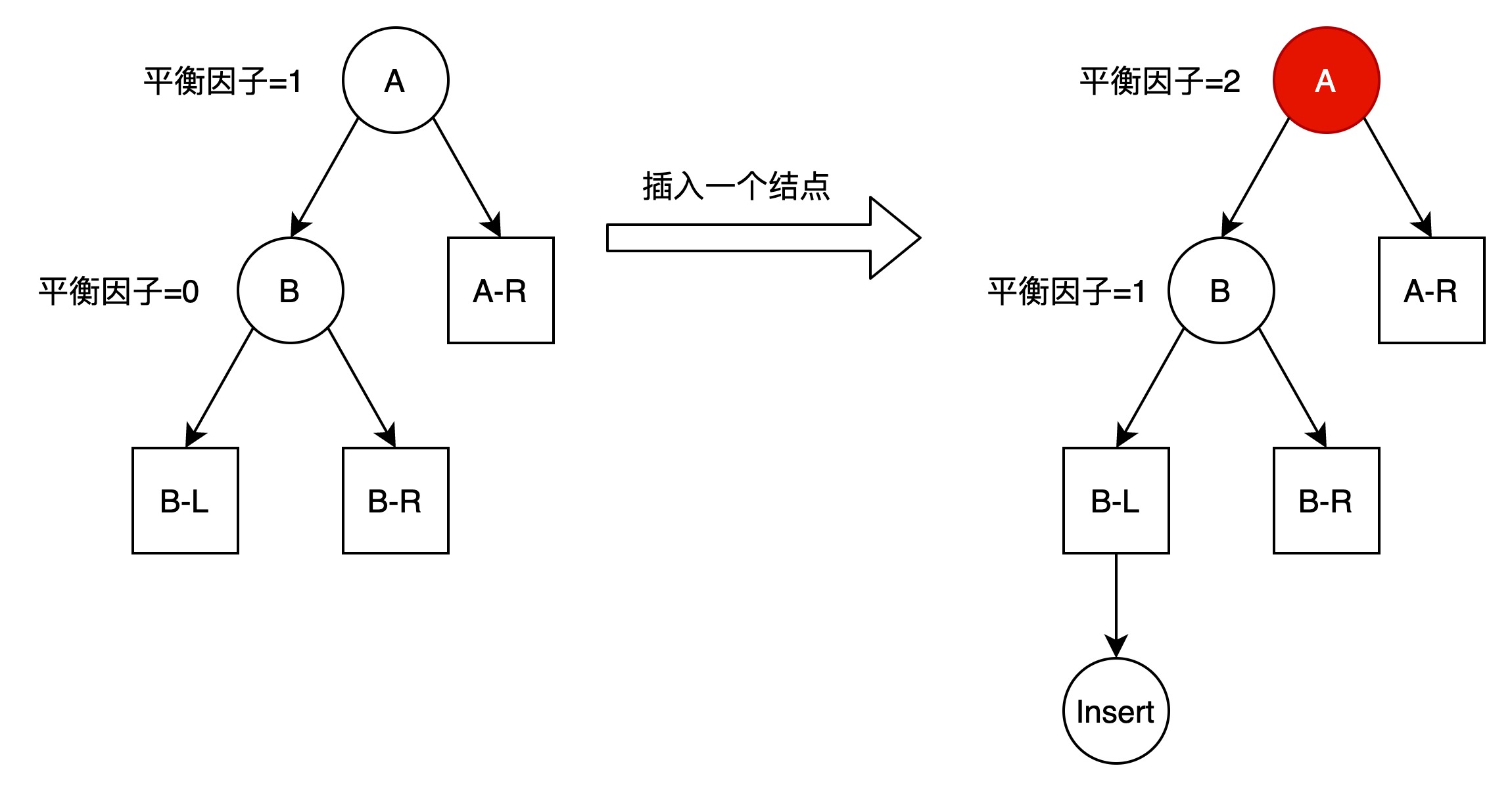
图中,A-R子树、B-L子树、B-R子树高度相等。
2.2.1.2.LL场景单旋转解决方案
可通过单旋转解决LL场景平衡问题,如下图所示:
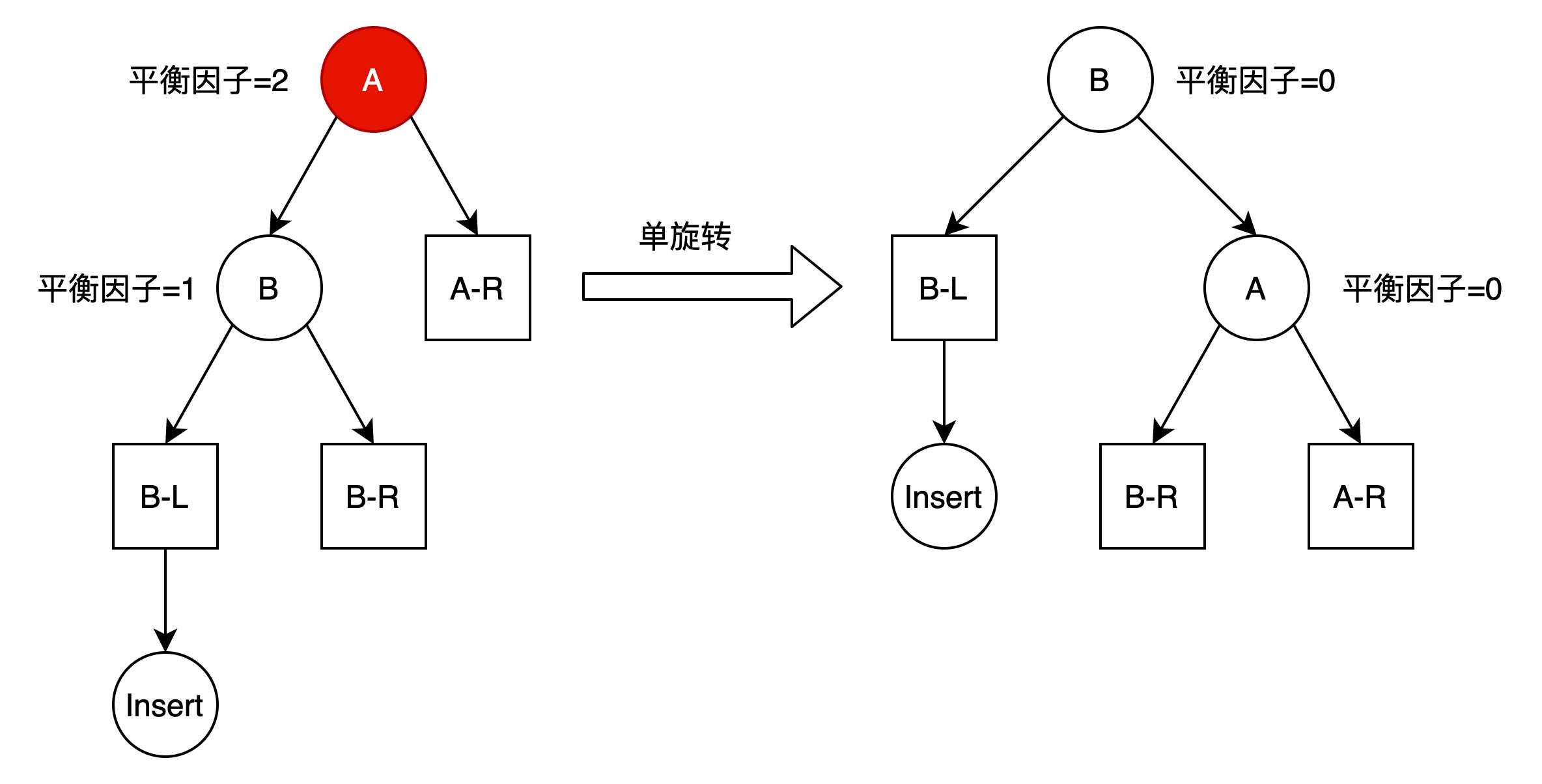
相当于A结点绕B结点顺时针旋转。
2.2.1.3.LL解决方案算法
算法伪代码如下:
p = root的左儿子
root的左儿子 = p的右儿子
p的右儿子 = root
将p设为树根 root = p2.2.2.LR场景
原来A得左子树比右子树高,插入发生在A的左儿子的右子树中,使A得左子树增高。
2.2.2.1.LR场景图示
如下图所示:
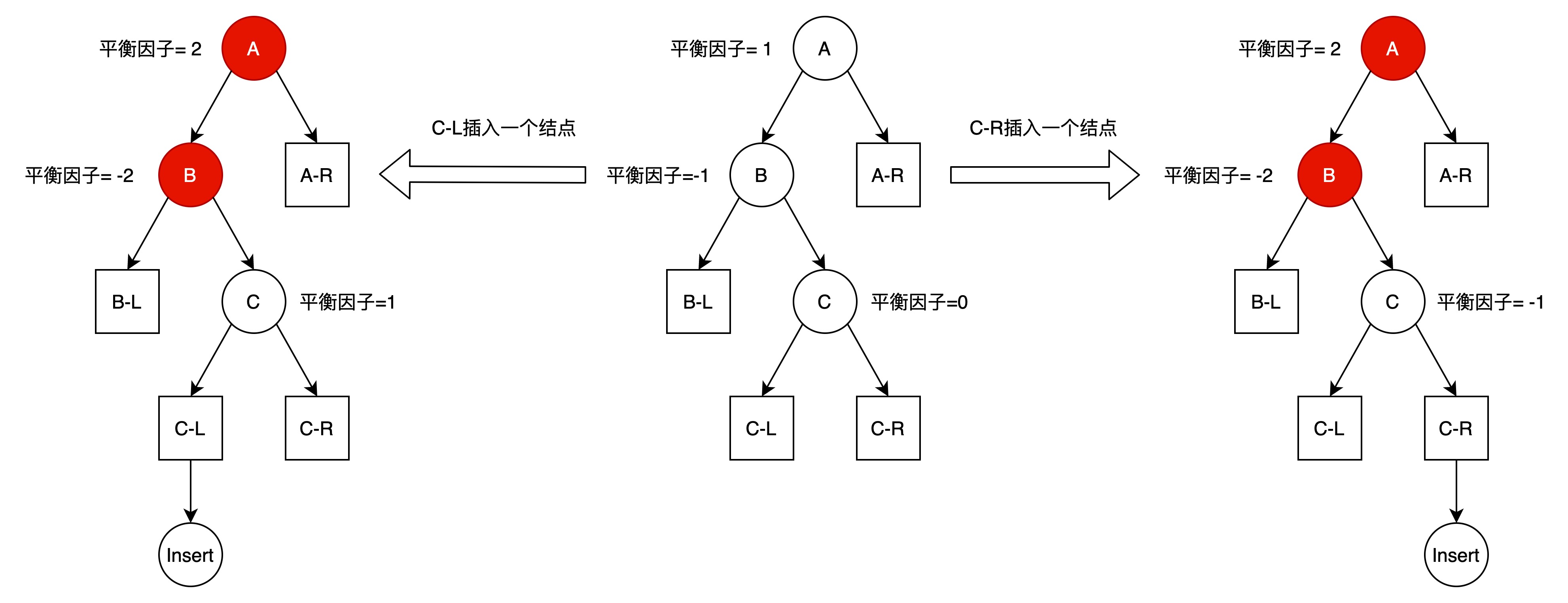
插入发生在B的右子树中,可以是C-L子树,也可以是C-R子树。
2.2.2.2.LR场景双旋转解决方案
通过两次旋转来解决LR场景平衡问题。如下图所示:
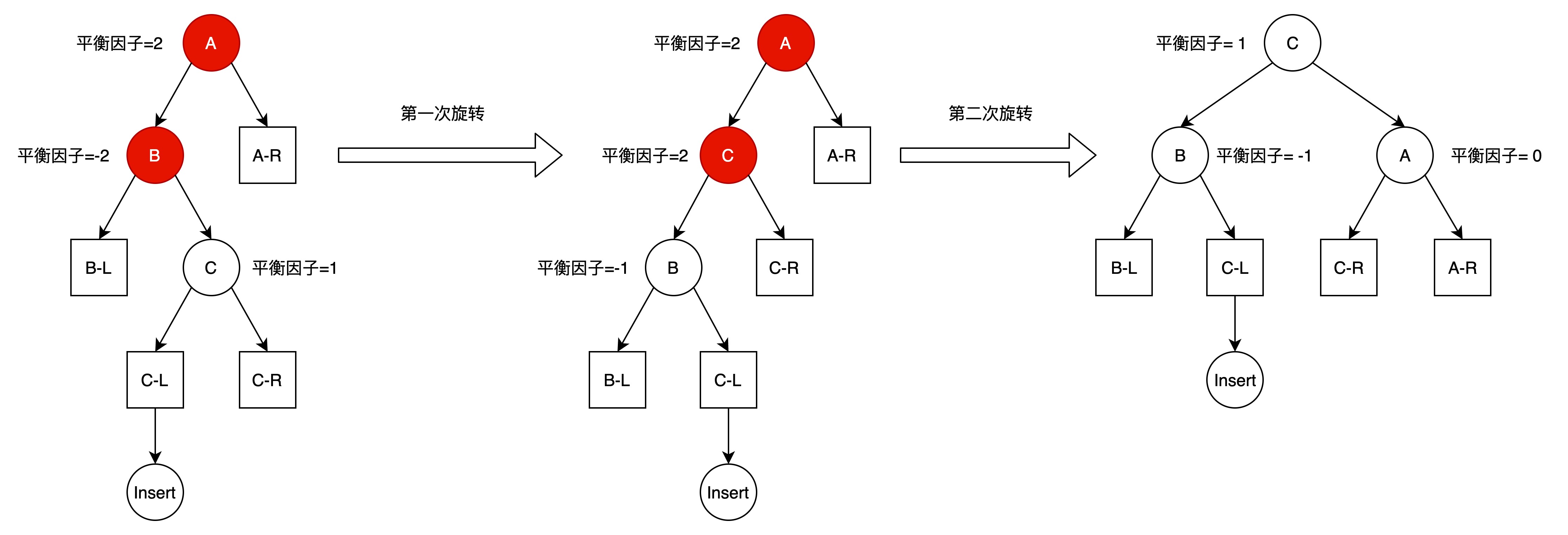
第一次旋转可看成是结点C围绕结点B逆时针旋转。
第二次旋转可以看成是结点A围绕结点C顺时针旋转。
2.2.2.3.LR解决方案算法
算法伪代码如下所示:
root的左儿子 = RR(root的左儿子)
root = LL(root)利用单旋转实现双旋转
2.2.3.RL场景
原来A得右子树比左子树高,插入发生在A的右儿子的左子树中,使A得右子树增高。
RL场景可看成是LR场景的镜像。
2.2.3.1.RL场景图示
如下图所示:
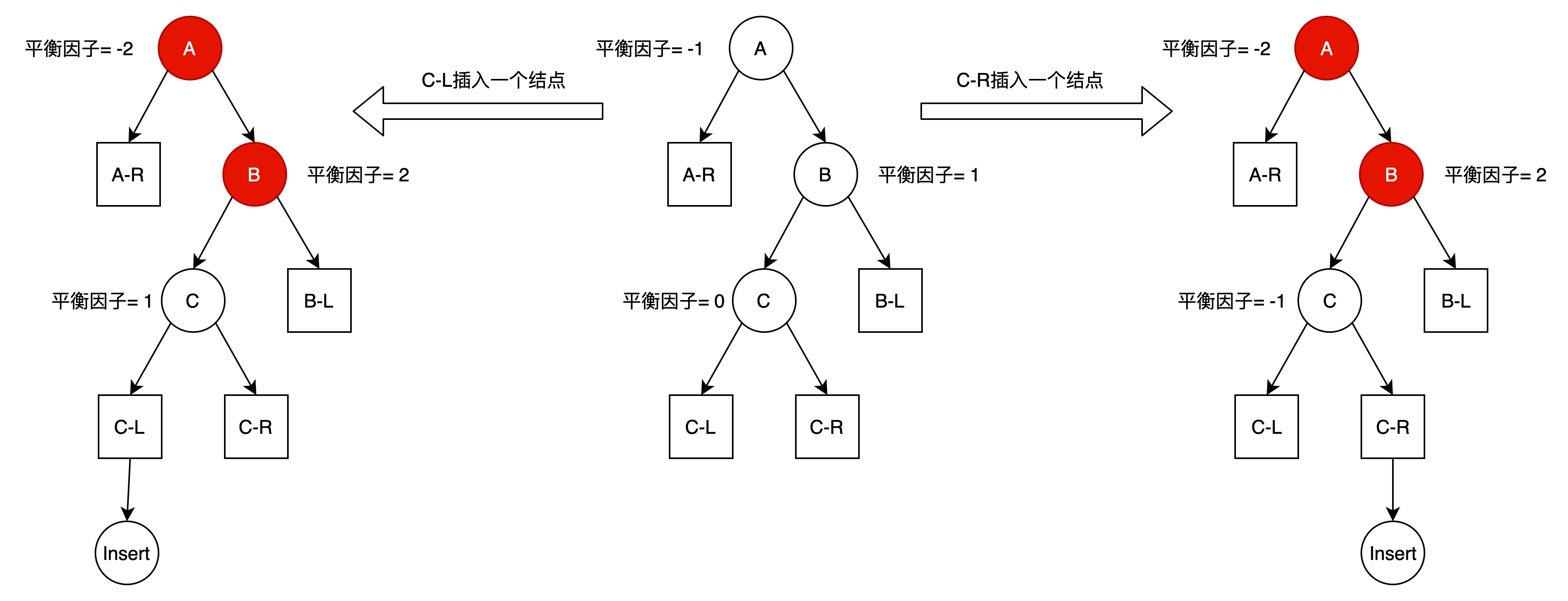
图中,A-R和B-L子树高度相等。
2.2.3.2.RL解决方案算法
算法伪代码如下所示:
root的右儿子 = LL(root的右儿子)
root = RR(root)利用单旋转实现双旋转
2.2.4.RR场景
原来A的右子树比左子树高,插入操作发生在A的右儿子的右子树中,使得A的右子树增高。
2.2.4.1.RR场景图示
如下图所示:
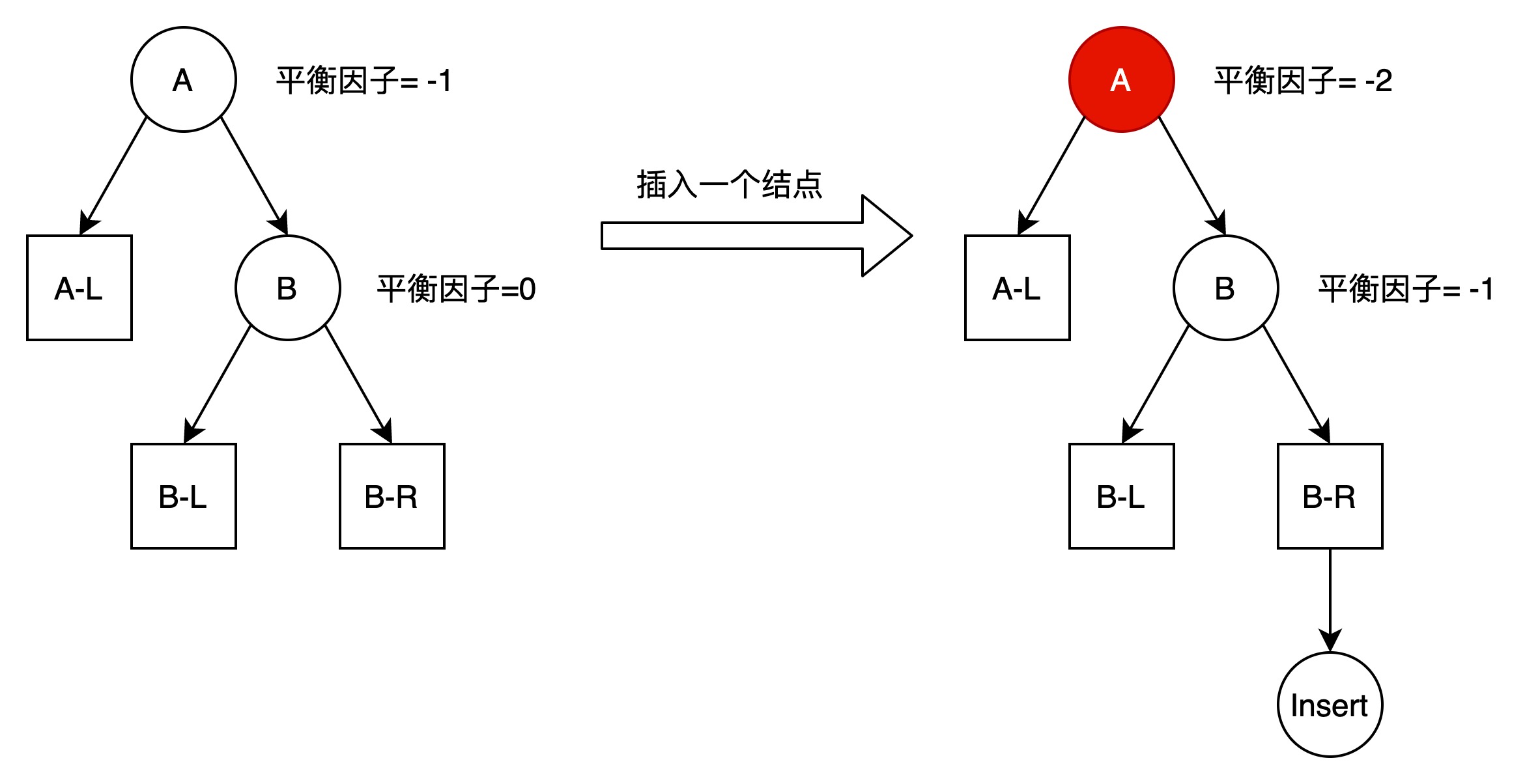
图中,A-L子树、B-L子树、B-R子树高度相等。
2.2.4.2.RR场景单旋转解决方案
通过单旋转解决RR平衡问题。与LL类似,不过旋转方向相反。
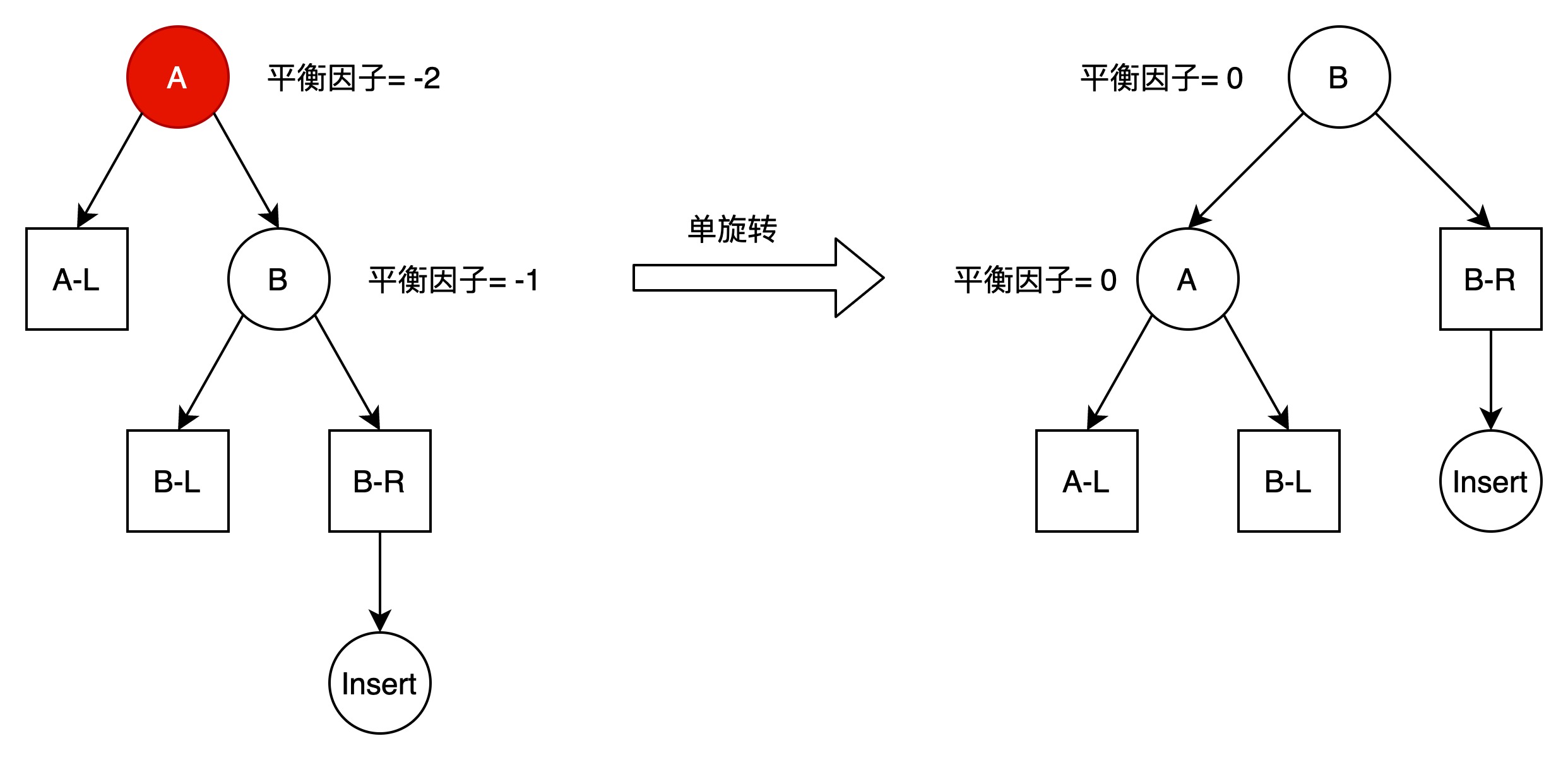
相当于A结点绕B结点逆时针旋转。
2.2.4.3.RR解决方案算法
算法伪代码如下:
p = root的右儿子
root的右儿子 = p的左儿子
p的左儿子 = root
将p设为树根 root = p2.3.remove
AVL树的删除操作分为两步:第一步数据结点插入;第二步结点平衡。
在第一步数据结点插入过程中,操作算法与二叉查找树完全一致。有