1.选择排序的定义

有N个待排序的元素，首先选出这N个元素中最小（大）的，然后从剩下的N-1个元素中选出最小（大）的，依次类推，经过N-1次选择后，我们就得到了一个有序的N个元素的序列。

从一个集合中选择最小（大）的算法有很多。

2.直接选择排序算法

直接选择排序是最简单的选择排序。

从所有元素中采用逐个比较的方法，选出最小元素，将最小元素与第一个元素进行交换。依此类推，经过N-1轮比较和交换后，所有元素都在正确的位置。

2.1.算法代码实现

如下所示：

    public void simpleSelectSort(T[] a, int size) {
        int k;
        T tmp;
        for (int i = 0; i < size - 1; i++) {
            k = i;
            for (int j = i + 1; j < size; ++j) {
                // 找到最小值
                if (a[j] < a[k]) {
                    k = j;
                }
            }
            // 将a[i]和a[k]进行交换
            tmp = a[i];
            a[i] = a[k];
            a[k] = tmp;
        }
    }

2.2.算法优点

主要有以下两点：

（1）直接选择排序算法简单

（2）额外的空间复杂度为O(1)

2.3.算法缺点

算法的实现涉及两个过程：比较和交换。

比较次数是固定的，如果有N个元素，需要进行N*(N-1)/2次比较。

交换次数不固定。最好的情况下，当前序列已经是有序的，则需要0次交换。最坏情况下，当前序列是逆序的，则需要N-1次交换。

所以算法的时间复杂度为O(N^2)。

3.直接选择排序的过程

通过案例来说明直接选择排序的过程。

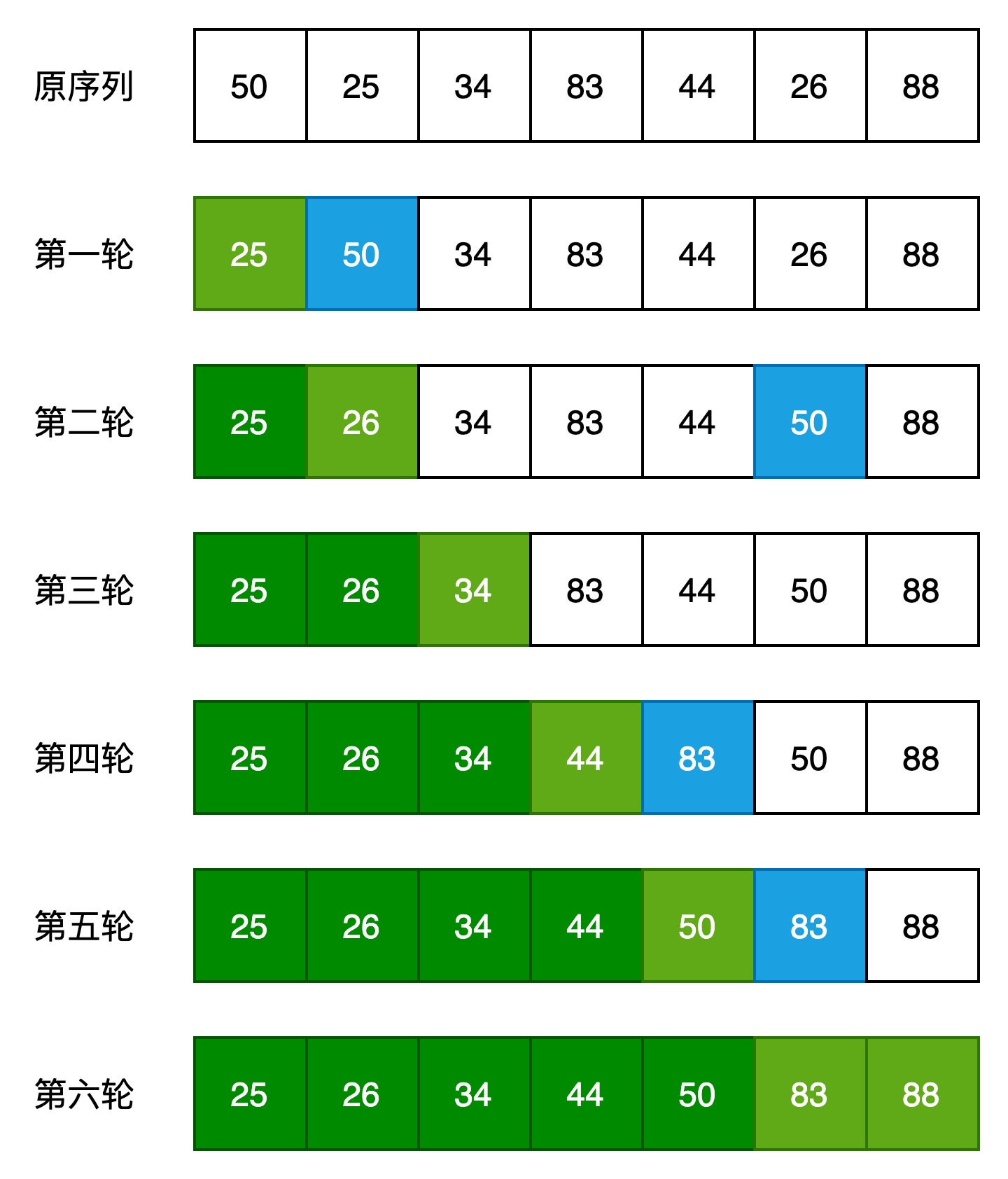
序列中有7个元素，经过6轮比较和交换后，得到了顺序的序列。