1.希尔排序的由来

希尔排序是直接插入排序的改良品种，尽管不是最快的，但是时间复杂度比O(N^2)要好。

希尔排序是Donald Shell在1959年设计的。

在直接插入排序中，元素的移动都是向后移动一位。如果一个结点与它正确的位置想差很远，则需要移动多次才能到达正确的位置上。这就造成了直接插入排序的高代价。

二分插入排序通过减少比较次数来提升排序效率。

希尔排序通过减少移动次数来提升排序效率。

2.希尔排序算法过程

希尔排序的想法是：先比较那些离得较远的元素，如果稍远的两个元素违反了次序，则进行交换。然后再比较那些离得较近的元素，两个元素的距离是一个递减序列。

算法过程如下：

（1）设计一个增量序列{h1, h2, ……, hn}

（2）对数组a进行间隔为hn的排序

a[0]、a[hn]、a[2hn]……为一组进行排序

a[1]、a[hn + 1]、a[2hn + 1]……为一组进行排序

……

a[hn - 1]、a[2hn - 1]、a[3hn - 1]……为一组进行排序

（3）依次对数组a进行间隔为hn到h1的排序。

（4）完成间隔为h1的排序后，最终得到一个有序数组。

代码如下所示：

    void shellSort(Comparable[] arr) {
        int j;
        for (int gap = arr.length / 2; gap >  0; gap /= 2) {
            for (int i = gap; i < arr.length; i++) {
                Comparable tmp = arr[i];
                for (j = i; j >= gap && tmp.compareTo(arr[j - gap]) < 0; j -= gap) {
                    arr[j] = arr[j - gap];
                }
                arr[j] = tmp;
            }
        }
    }

3.希尔排序性能

希尔排序的增量序列可有多种不同的取法，但是最后一个间隔必须为1，即h1 = 1。

D.E.Knuth利用大量实验统计资料得出：当待排序数组元素个数N很大时，元素的移动次数大约为N^1.25~1.6*N^1.25

4.希尔排序案例

例如以下数组，增量序列为{1,3,5}，则排序过程如下图所示：

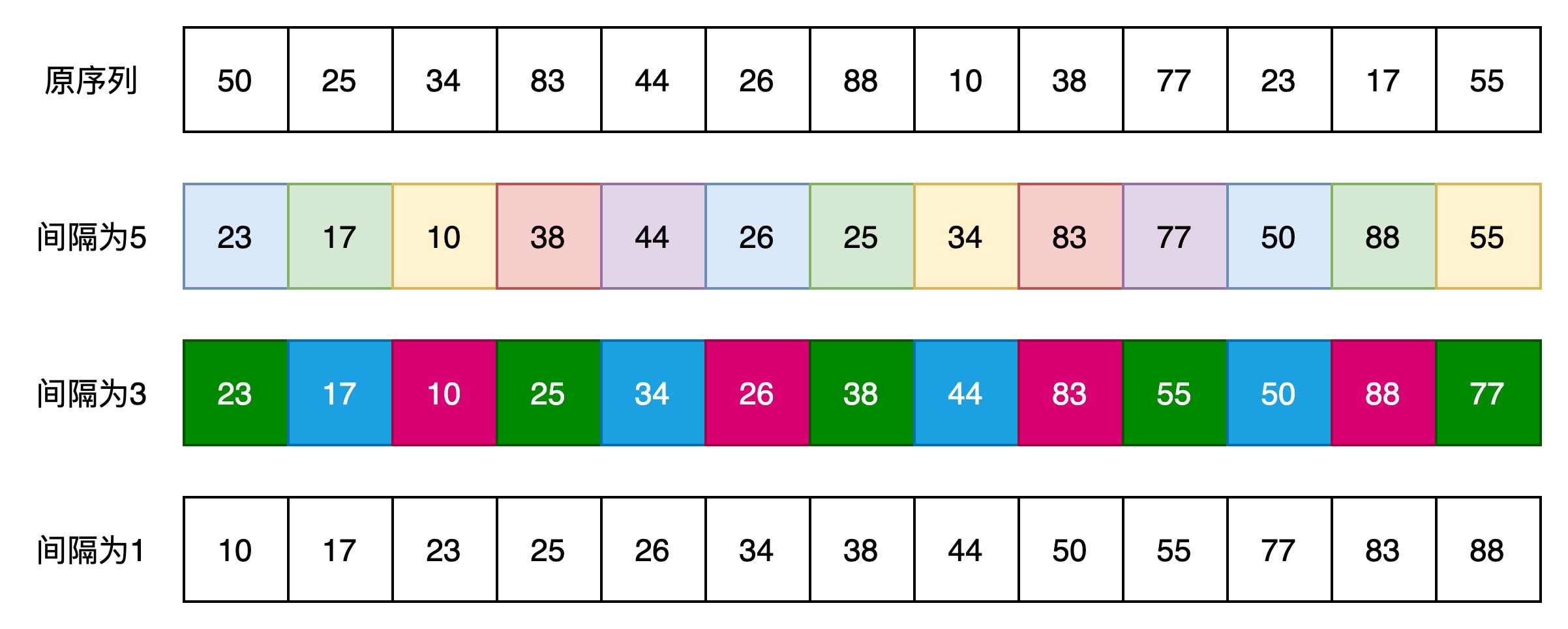
（1）间隔为5，分别对以下序列进行排序

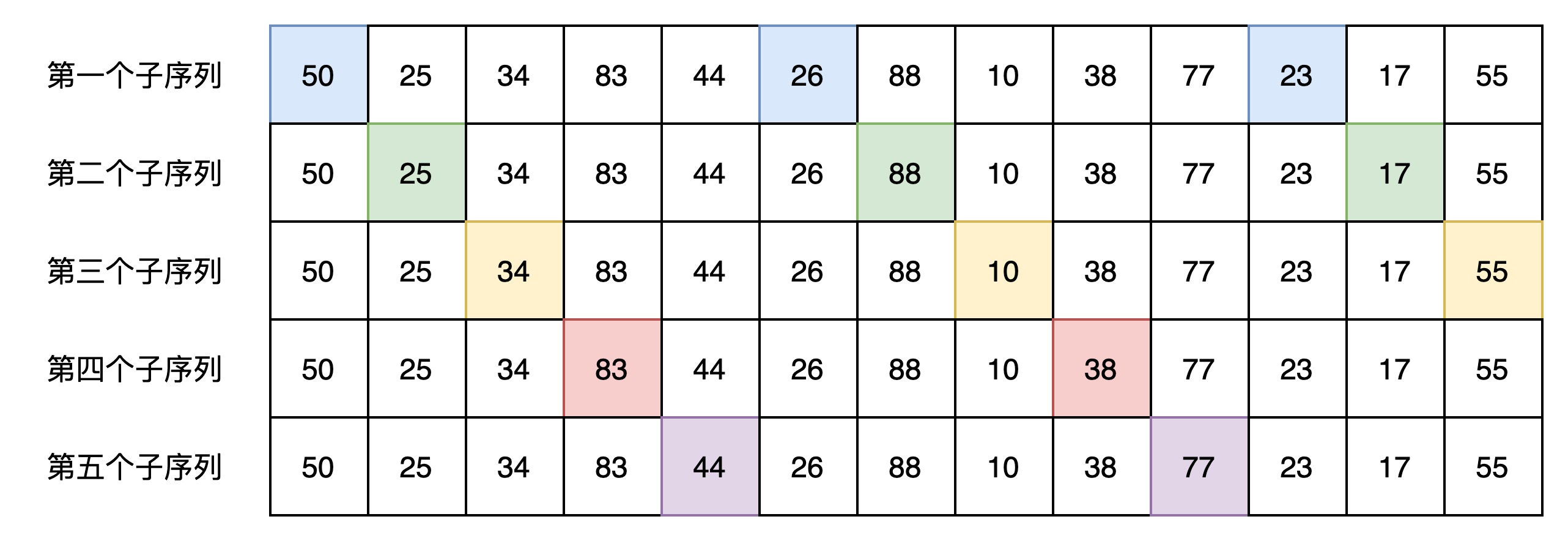
（2）间隔为5，分别对以下序列进行排序

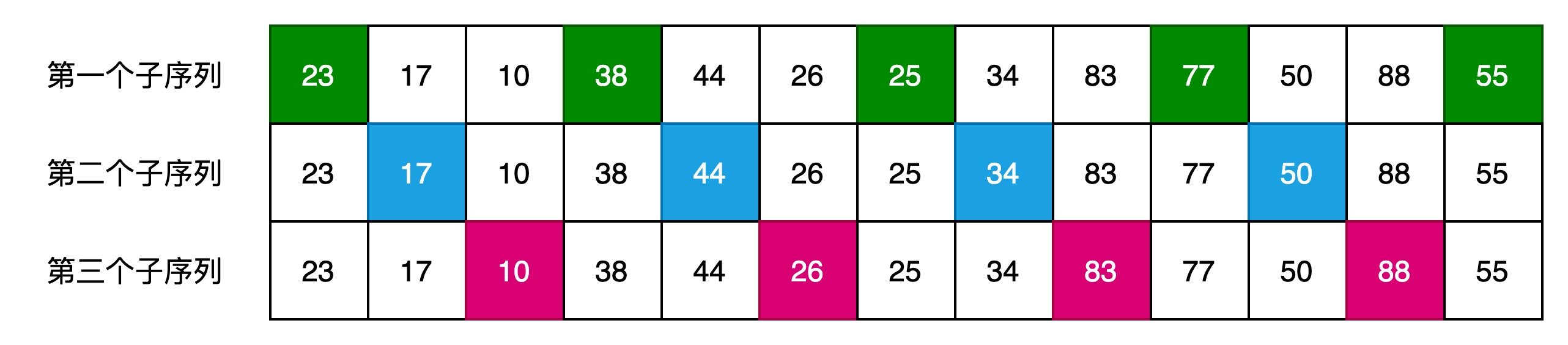
（3）间隔为1，对整个序列排序

排序完成