1.二叉树概述
Binary Tree
1.1.二叉树的定义
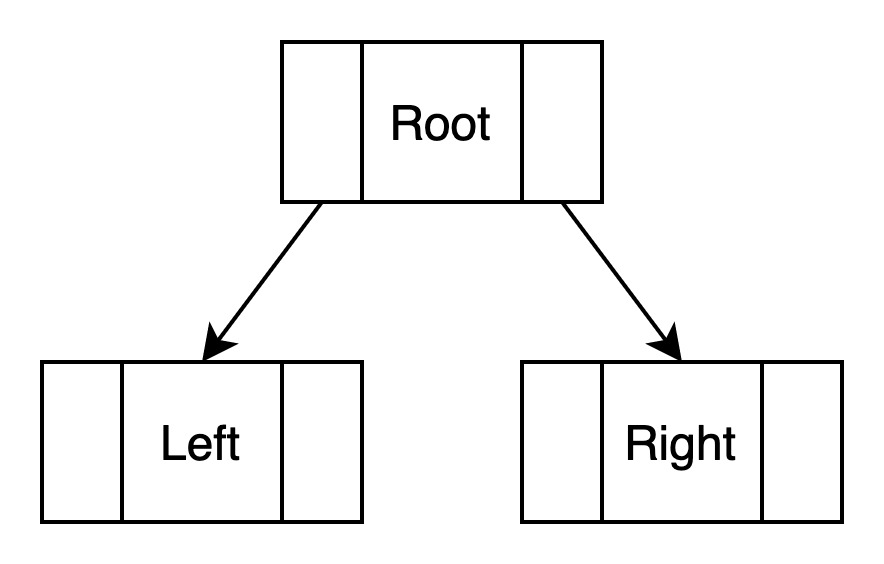
二叉树是结点的有限集合,它可以为空树,或者是根结点和两个互不相交的子树构成,其左右两个子树都是二叉树。
二叉树是有序树,必须严格区分左右子树。
如下图所示:
1.2.二叉树的操作
二叉树的运算比较多。
(1)create:创建二叉树
(2)clear:清空二叉树所有结点
(3)isEmpty:二叉树是否为空树
(4)root:二叉树的根结点
(5)parent:找某个节点的父结点
(6)lchild:找某个节点的左儿子结点
(7)rchild:找某个节点的右儿子结点
(8)delLeft:删除某个节点的左子树
(9)delRight:删除某个节点的右子树
(10)traverse:遍历二叉树上的每一个节点
1.3.二叉树的遍历
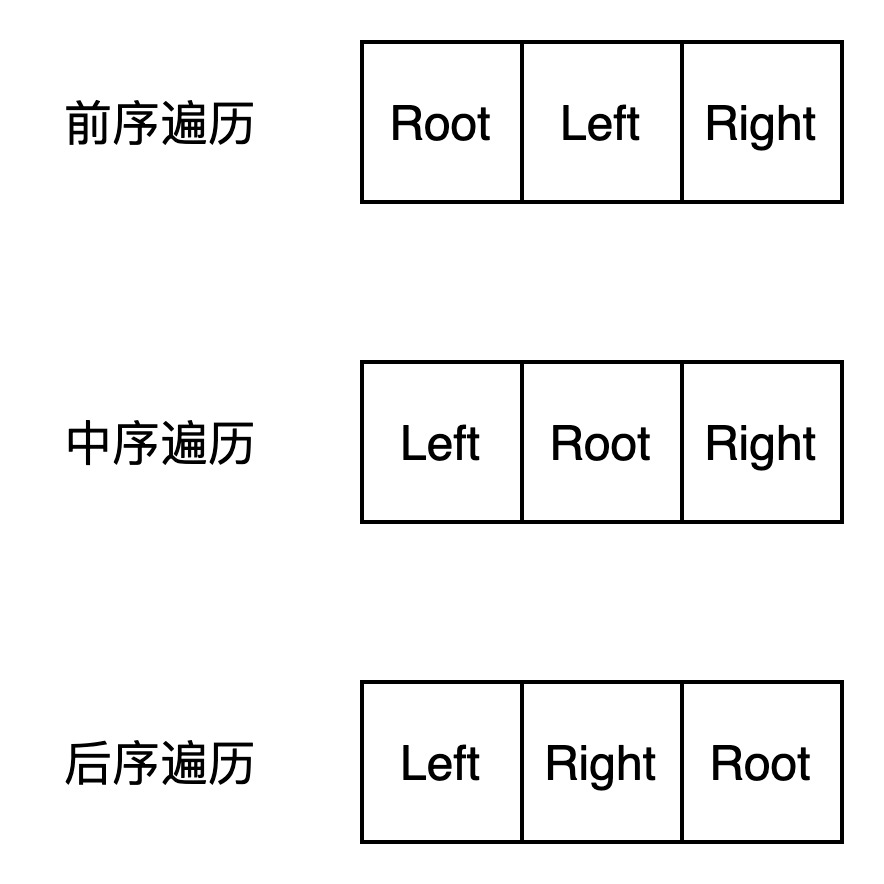
二叉树有三种遍历方式。
1.3.1.前序遍历
先访问根结点,再访问左子树,最后访问右子树
1.3.2.中序遍历
先访问左子树,再访问根结点,最后访问右子树
1.3.3.后序遍历
先访问左子树,然后访问右子树,最后访问根结点
1.4.满二叉树
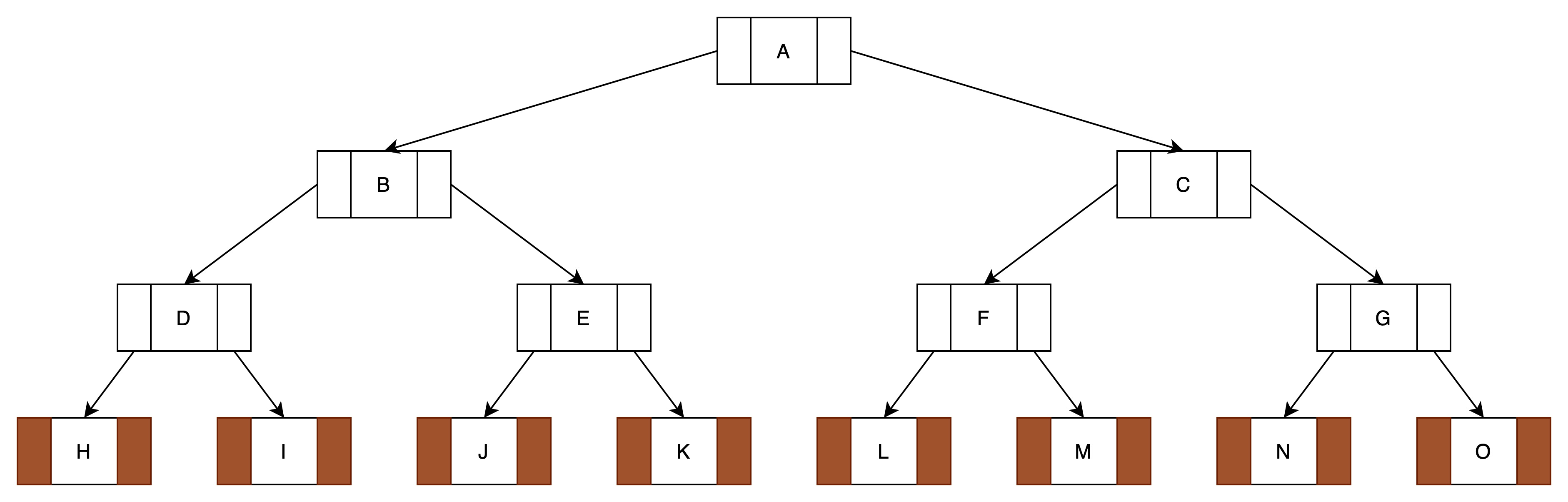
又叫丰满树,二叉树中任意一层的结点数都达到了最大值。
如下图所示:
1.5.完全二叉树
完全二叉树是满二叉树的最底层从右到左连续剪除若干个节点。
所以,满二叉树也是完全二叉树。
完全二叉树例如下图所示:
2.二叉树的顺序实现
顺序存储就是将节点存放在数组中,通过数组下标之间的关系表示数据元素之间的父子关系。
二叉树如何转换为数组存储?下面通过案例来说明
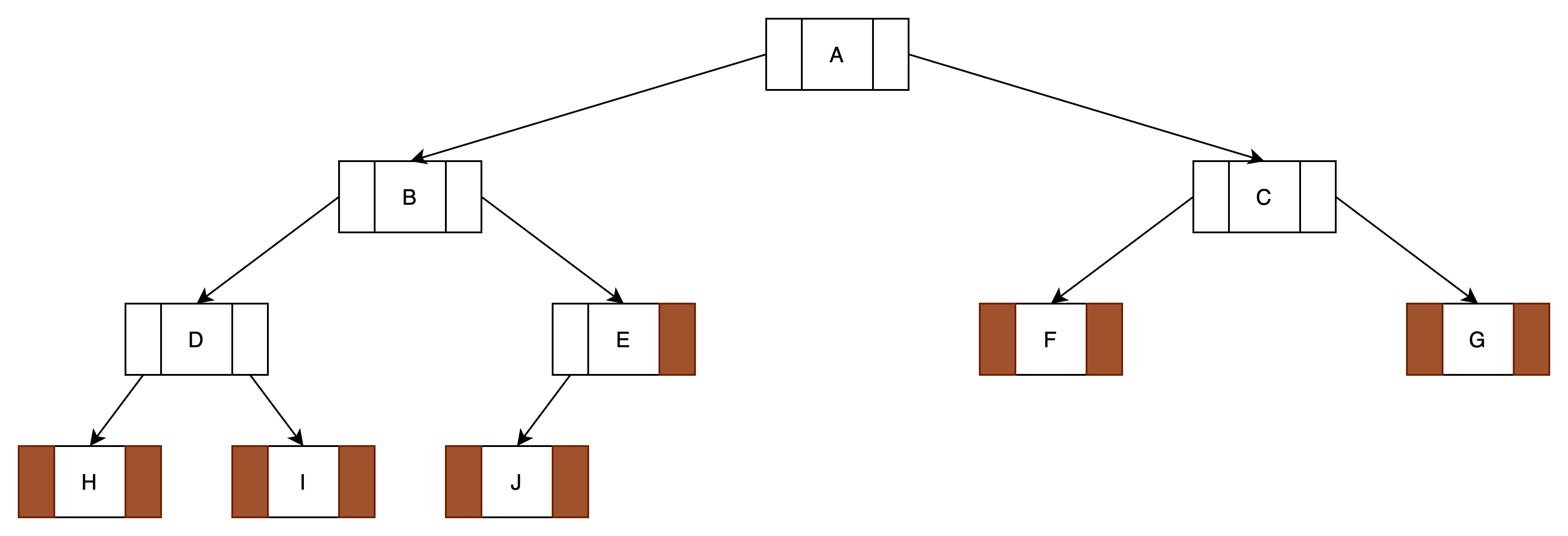
(1)构造一个二叉树
(2)将此二叉树补充为一颗完全二叉树
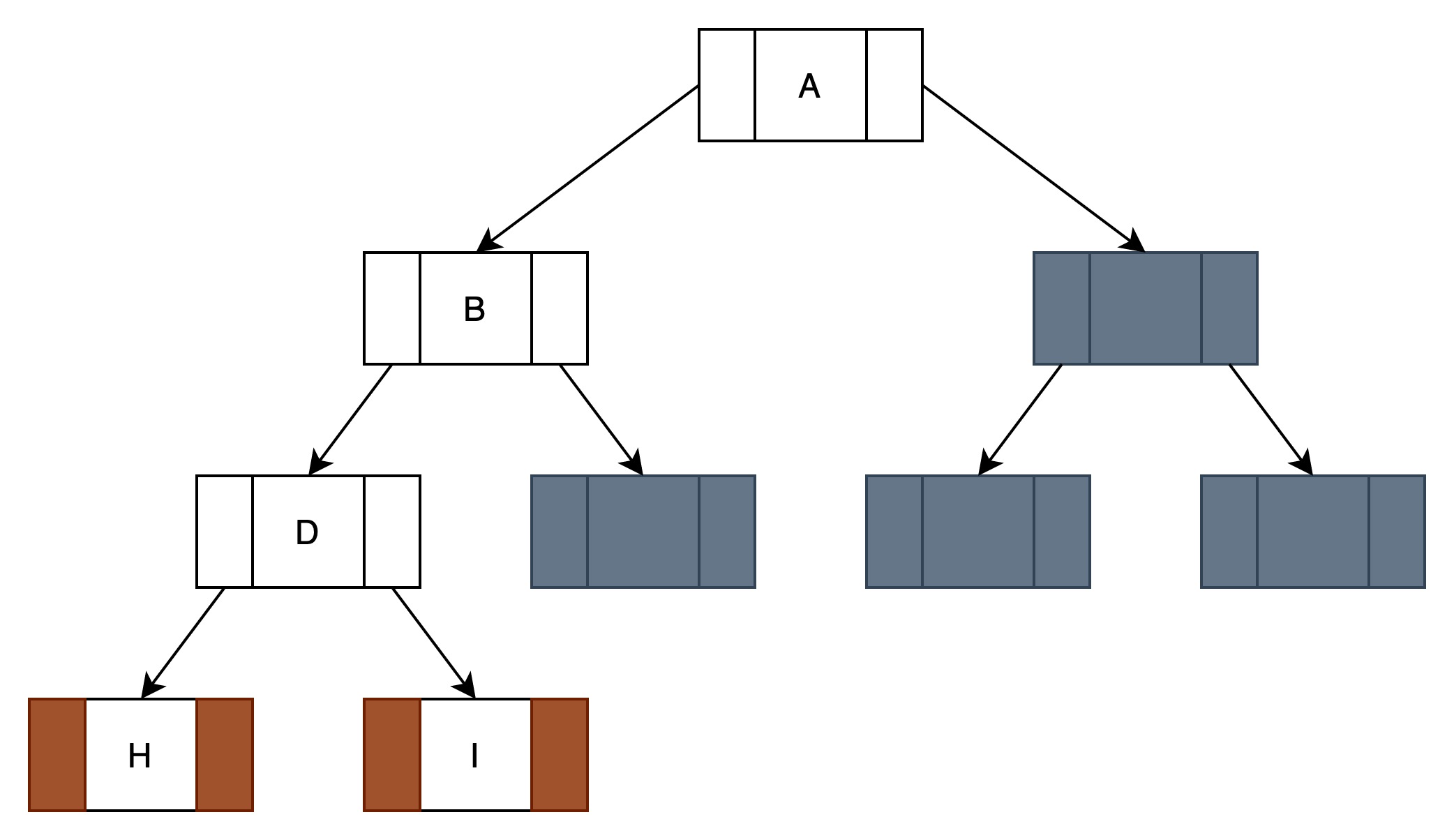
补充了4个节点(灰色)。
(3)将完全二叉树转换为数组

这里数组存储的下标从1开始。下标0不存放任何数据。
这里可以看出,对于数组中下标为k的结点,,其父结点是数组中下标为k/2的元素,其左结点下标为2k,右结点下标为2k+1
3.二叉树的链表实现
二叉树的链表有两种表现形式。
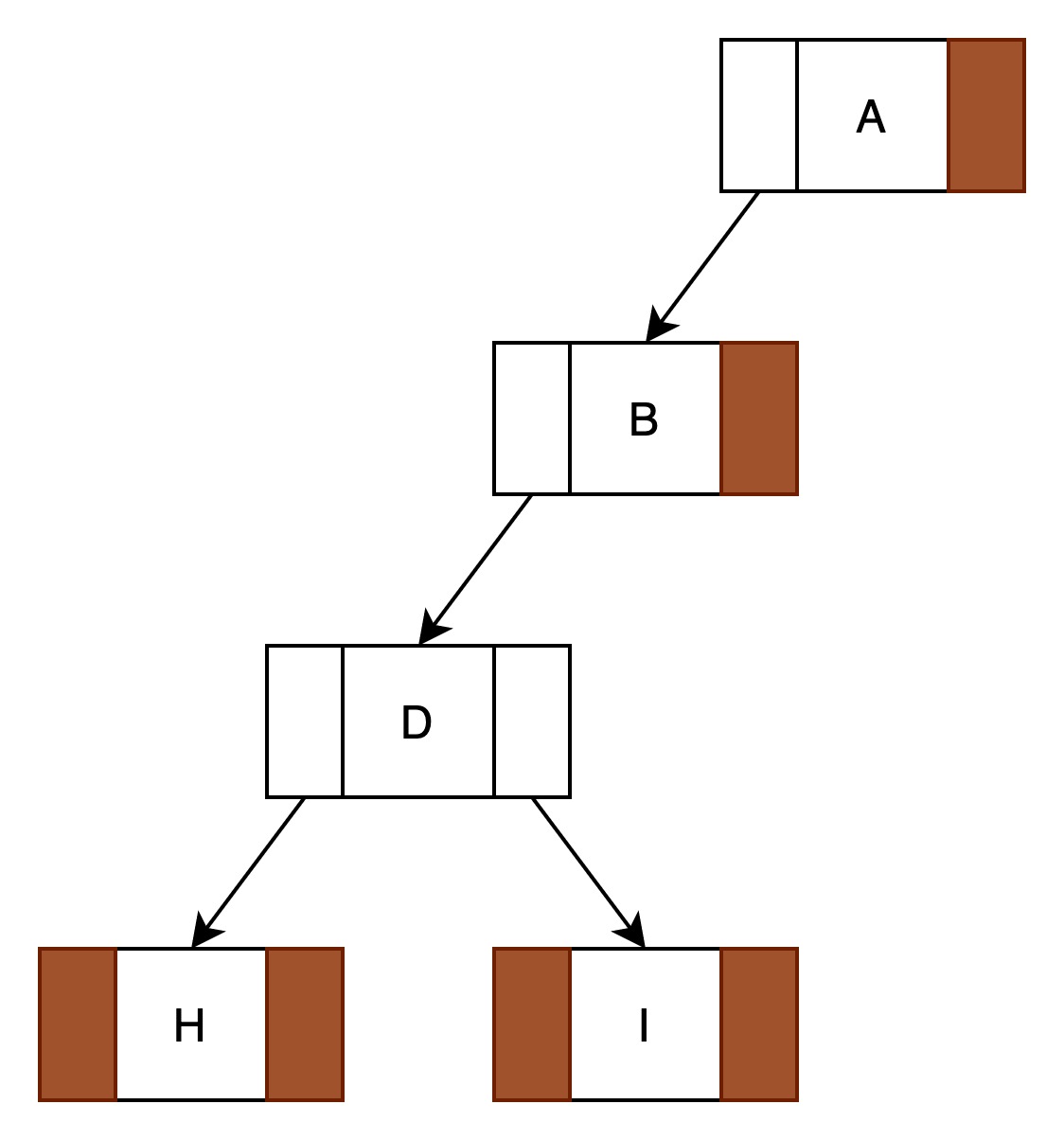
3.1.二叉链表
也是标准存储结构。
结点结构如下图所示:

每个元素有两个引用,分别指向左子树和右子树。
二叉链表例如下图所示:
共有8个结点,或者说8个元素。
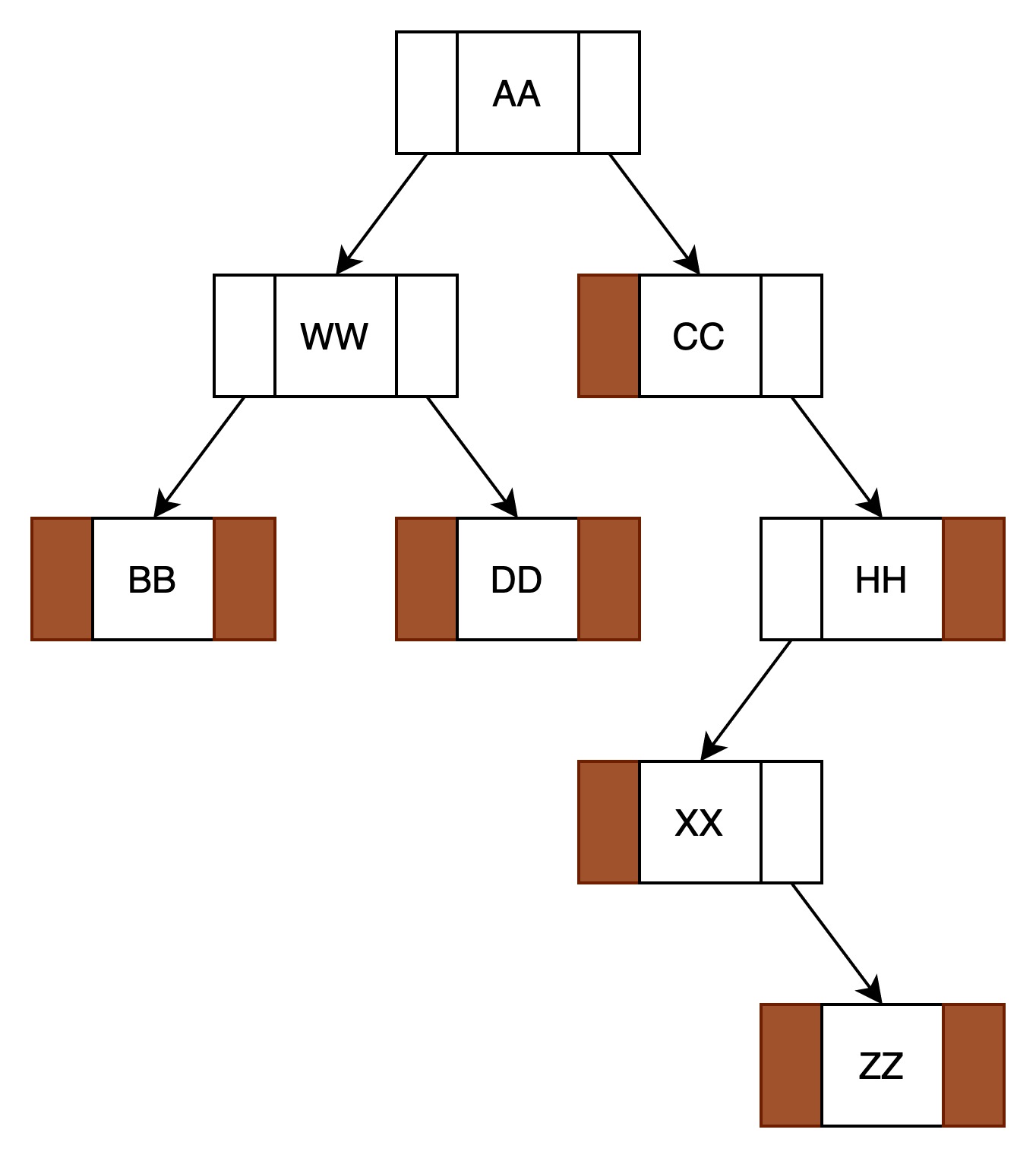
3.2.三叉链表
被称为广义存储结构。
结点结构如下图所示:
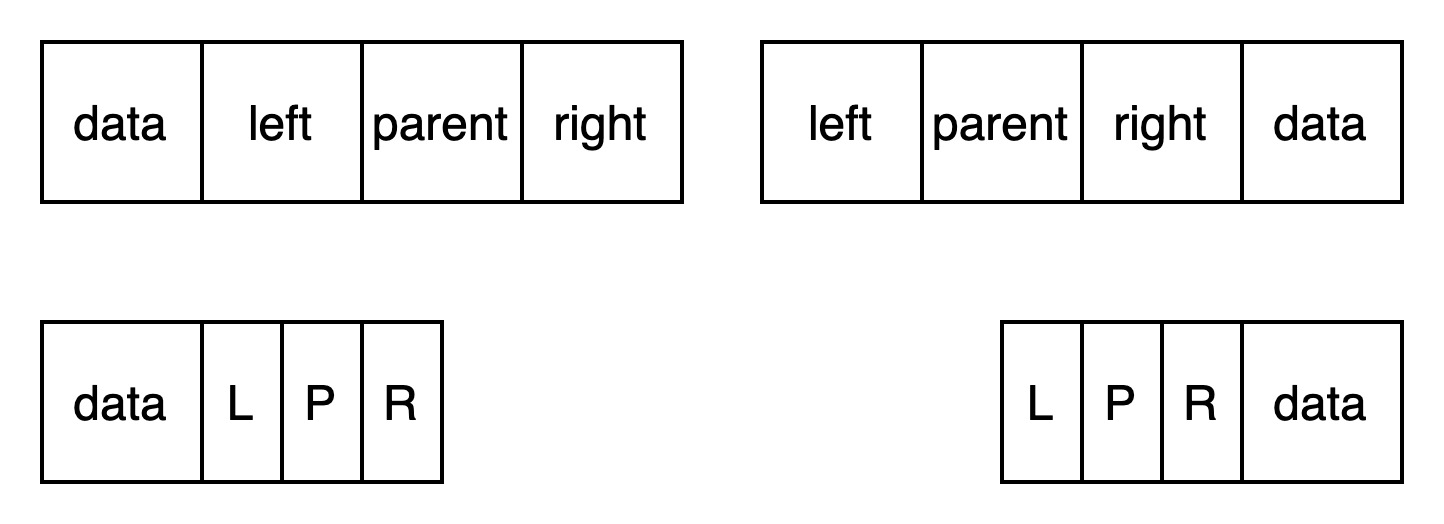
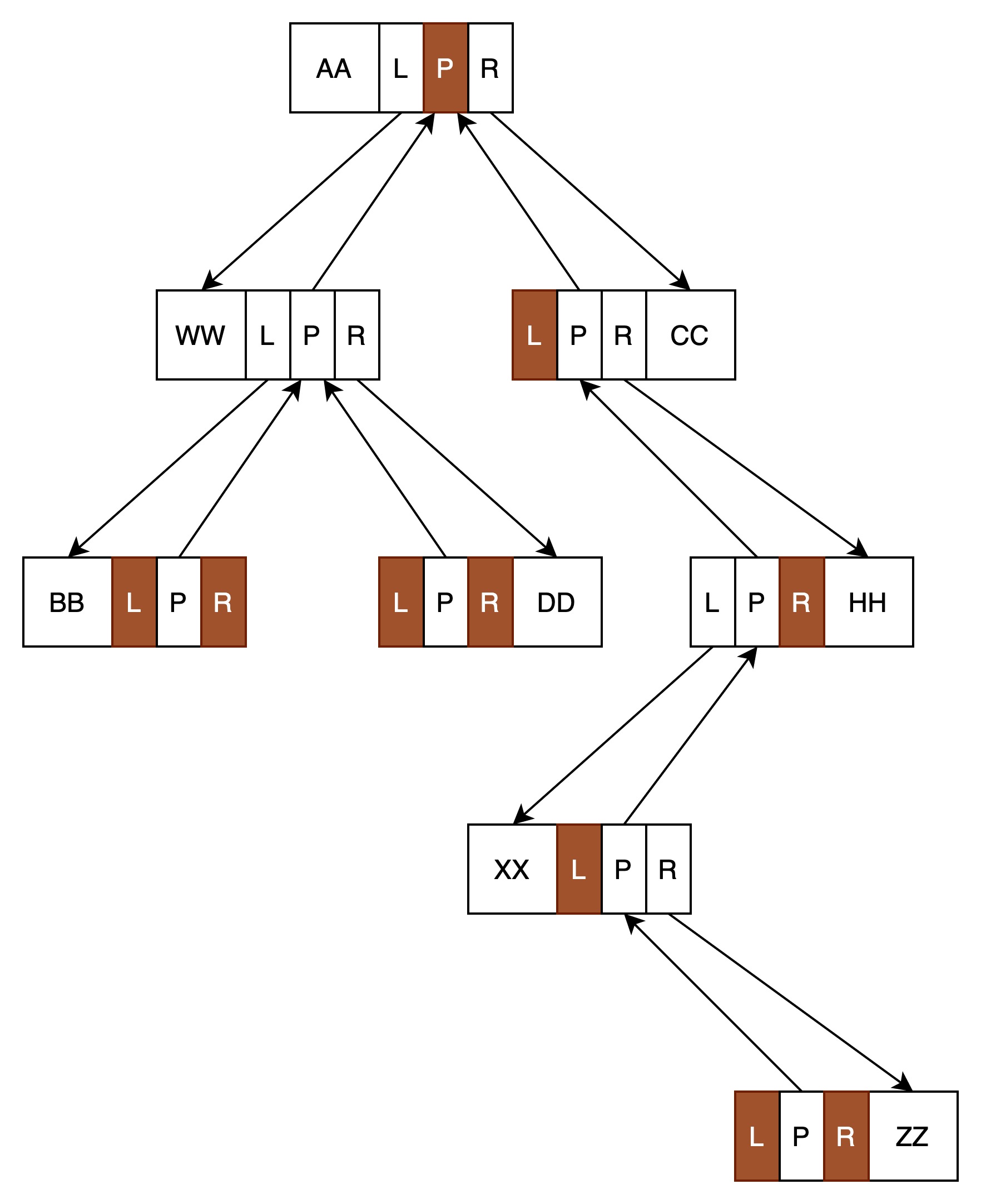
每个元素有三个引用,分别指向左子树(L)、右子树(R)、父结点(P)。
三叉链表例如下图所示: