1.基数统计场景

一个（有限）集合S里不同的元素个数就称为该集合的基数（cardinality），也叫做“势”，记为|S|。

例如，S={"小明", "小明", "小刚", "小红", "小红", "小明"}，那么|S|=3。

日常生活中，常有需要基数统计的场景，比如DAU——日活跃用户数，DAU是衡量1互联网产品活跃度最直接的指标。

2.Linear Counting(LC)

Linear Counting（线性计数）算法由Kyu-Young Whang等人在1990年的论文《A Linear-Time Probabilistic Counting Algorithm for Database Applications》中提出。论文可参考https://dblab.kaist.ac.kr/Prof/pdf/ACM90_TODS_v15n2.pdf

算法流程如下：

（1）创建一个有m个bit的位数组，初始状态是0填充的。

（2）设定一个哈希函数H，它的结果空间正好落在上述位数组中，尽量服从均匀分布，并且按每bit分桶。

（3）将集合C的元素依次输入H，散列到位数组中，将其散列到的bit置为1。

（4）所有元素输入完成后，且位数组中仍然为0的bit（即空桶）共有u个，那么基数的一个估计公式如下：

|C| = -m * ln(u / m)

论文给了算法的样例，如下图所示：

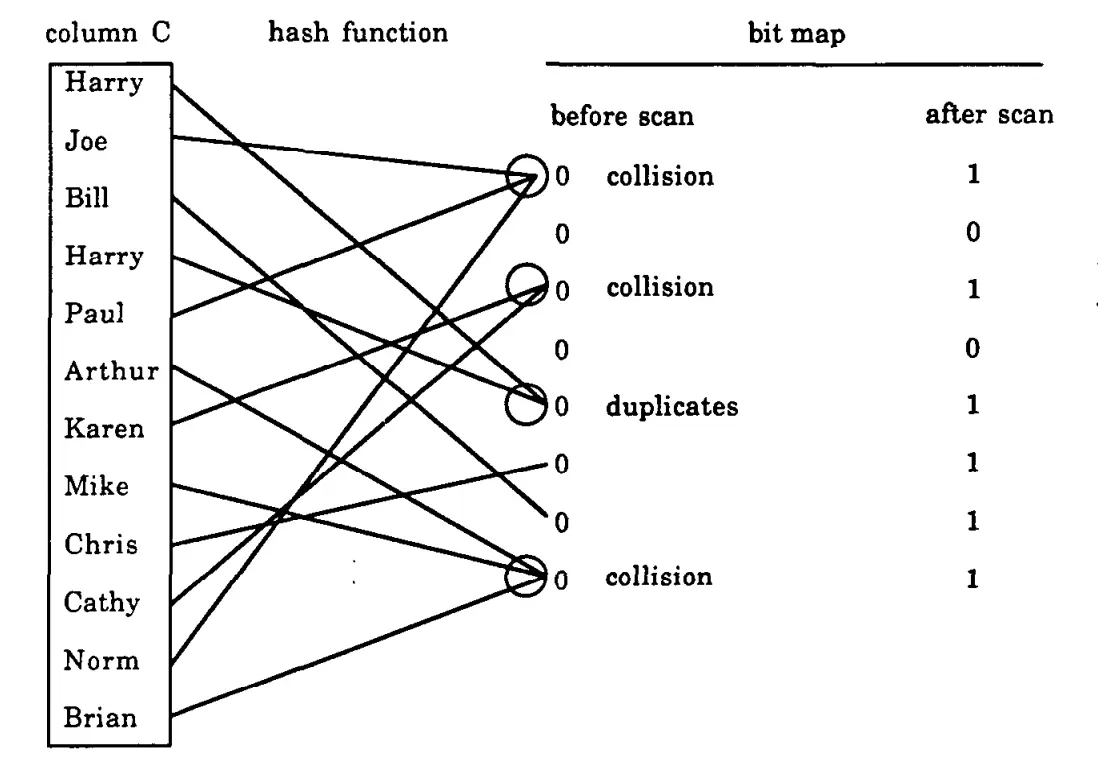
最后基数估算=-8 * ln(2 / 8) = 11

3.LogLog Counting(LLC)

日志统计

4.HyperLogLog Counting(HLL)

基数估计已经有了多种成熟的实现，应用比较广泛的就是HyperLogLog

5.Flajolet-Martin

这个算法由Philippe Flajolet和G.Nigel Martin在1984年的论文《Probabilistic Counting Algorithms for Data Base Applications》中提出，论文可参考https://algo.inria.fr/flajolet/Publications/FlMa85.pdf

算法的流程如下：

（1）初始化一个长度为L的位数组，记为bitmap[0...L-1]，用0填充。

（2）计算基数的集合为M，共有n个元素，每个元素通过M(i)表示，0=<i<=n-1。将bitmap[p(H(x))]设为1。H表示hash函数，p表示散列函数。

（3）令R表示哈希过后bitmap中所有0的最小的下标，那么|M|的估计量为2^R/c，c是常数，约等于0.77351。